-
医学研究中进行一致性检验时,通常有以下方法如下表:
方法 数据类型 功能倾重 其它 ICC组内相关系数 定量或定类 一致性测量 N个数据一致性 Kappa一致性系数 定类(或定序等级数据) 一致性测量 仅针对2项数据一致性 Kendall W协调系数 定量(或定序等级数据) 关联程度测量 N个数据关联程度 Bland-Altman图 定量数据 一致性测量 仅针对2项数据一致性 首先从数据类型适用性上判断:ICC适用于定量或定类数据均可;但是Kappa一致性系数通常用于定类数据一致性;以及Kendall W协调系数用于定量数据,尤其是定序等级数据。
举例场景说明:
-
场景1:3个医生对于10个病人的智商分值一致性
-
此类情况可使用ICC,或者Kendall W协调系数,但一般会使用ICC,原因在于定量数据且测量一致性。
-
场景2:3个医生对于10个病人的疗效(分痊愈,显效,有效,无效)一致性
-
此类情况可使用ICC,Kendall W协调系数;数据上属于定序等级数据,可使用Kendall W协调系数,当然也可使用ICC。
-
场景3:2个医生对于10个病人的疗效(分痊愈,显效,有效,无效)一致性
-
此类情况可使用ICC,Kappa一致性系数,或者Kendall W协调系数;但一般可使用ICC或者Kappa一致性系数且加权。
-
场景4:2个医生对于10个病人的癌症诊断结果(分阳性和阴性)一致性
-
此类情况可使用ICC,Kappa一致性系数,但一般会使用Kappa一致性系数,原因在于定类数据且2组(2个医生),定类数据不能使用Kendall W协调系数。
-
场景5:2个医生对于10个病人的心跳测量值一致性
-
此类情况可使用ICC,Kendall W协调系数和Bland-Altman图。一般使用ICC,或Bland-Altman图较多。原因在于测量值为连续定量数据(不能使用Kappa),Kendall W更强调关联程度并非一致性。因而可使用Bland-Altman图进行查看一致性情况,Bland-Altman图是惟一可使用图形直观展示一致性的方法。
-
特别提示
-
一致性的测量有多种方法,通常是结合数据特征情况选择相对适合的进行即可,比如需要画图展示那使用Bland-Altman图,如果类别数据一致性测量可使用Kappa系数,如果是定量数据测量关联性那么就使用Kendall W协调系数等。各方法操作可在医学研究/实验模块中找到。
-
Bland-Altman图案例
-
1、背景
当前有医生使用两种方法分别做一项实验(针对20个研究对象),现需要对第1种和第2种方法共两种方法的测量数据进行一致性检验,数据结构如下图:
ID 第1种方法 第2种方法 1 10 8 2 1 6 3 9 5 4 2 1 5 10 1 6 5 7 7 7 8 8 2 7 9 1 2 10 10 4 11 7 8 12 7 1 13 1 2 14 1 2 15 3 2 16 9 1 17 7 4 18 3 10 19 6 3 20 9 7 -
2、理论
Bland-Altman图是一种一致性测量的可视化展示方法。其将测量数据相关计算后,进行散点展示出来,如果说散点在可信区间范围内(一般是差值的1.96个标准差范围内),那么就说明数据具有较好的一致性水平。
Bland-Altman图的横坐标为两种方法的平均值,纵坐标为两种方法的差值。比如有100个研究对象,每个对象进行两次测量,那么就会有100个平均值数据(两次测量的平均值),对应以及100个差值数据(两种方法的测量数据差值),将此100个数据散点展示,如果说此100个点介于“差值的95%区间即差值的1.96的标准差范围内”,此时说明具有非常好的一致性,但具体标准是全部点都在标准内,还有绝大多数点都在标准内即说明具有一致性,这将由参考文献决定。
同时,如果有分组数据,比如同一研究对象使用两种测量方法进行测量,并且研究对象可分成几个类别,此时只需要把类别group放入对应框中即可,group仅在图示中展示出不同的颜色进行区分,对于指标的计算并不会有任何的影响。
-
3、操作
本例子中测量两种方法的测量一致性问题(且并没有区分group类别),则操作如下:
-
4、SPSSAU输出结果
SPSSAU共输出1个表格和1个图;分别是“Bland-Altman描述统计”,“Bland-Altman描述统计图”。
Bland-Altman描述统计:其展示两个测量数据的平均值,以及差值的均值,差值的标准差,差值均值的95%置信区间,差值的95%置信区间,差值的显著性检验,同时SPSSAU还提供重复以血性系数CR值指标;显著性检验的原理为配对t检验,其用于检验差值是否明显偏离数字0,如果呈现出显著性,说明差值明显偏离数字0(即说明两种方法具有不一致性),反之说明差值不会明显偏离数字0(即说明两种方法具有一致性)。
Bland-Altman图:横坐标为两种方法测量数据的平均值,纵坐标为两种方法的测量差值,图中共包括3条线,中间线条表示差值的平均值,上下线条为95%一致性界限的上下限(即1.96个标准差上下界值)。
-
5、文字分析
Bland-Altman描述统计 项 值 有效样本量 20 均值(第1种方法) 5.500 均值(第2种方法) 4.450 均值(差值) 1.050 标准差(差值) 4.273 95% CI(差值均值) -0.950 ~ 3.050 95% CI(差值) -7.325 ~ 9.425 t 值(H0:差值的平均值=0) 1.099 p 值(H0:差值的平均值=0) 0.286 CR 值(Coefficient of Repeatability) 8.419 从上表可知:本次数据共有20个样本(测量对象),以及第1种方法和第2种方法测量的平均值分别是5.5和4.5,使用配对t检验显示,数据并没有呈现出显著性(p=0.286>0.05),即说明两种测量方法的差值并没有明显偏离数字0,也即说明两种测量方法具有一致性。两种测量方法差值的95%置信区间为-7.325 ~ 9.425,如果说Bland-Altman图中的散点纵坐标基于均介于此区间范围内,则说明数据具有良好的一致性水平。
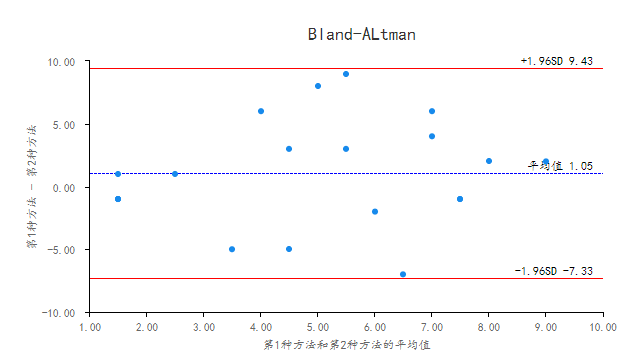
从Bland-Altman图可知,两种方法差值的均值为1.05,差值的95%置信区间为-7.33 ~ 9.43,所有测量数据均介于95%置信区间范围内,意味着本次数据具有良好的一致性水平。
如果说测量对象具有类别属性,而且希望在图中展示出类别效果。可将类别项放入对应框中,输出表格并不会有任何变化,但输出的Bland-Altman图中会用不同的颜色标识出不同的类别属性,类似如下图:
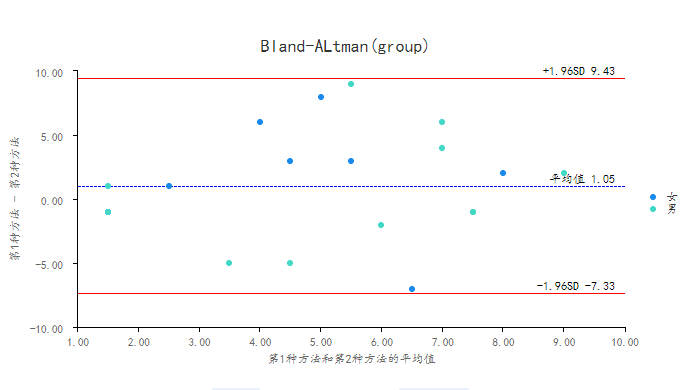
-
6、剖析
涉及以下几个关键点,分别如下:
-
Bland-Altman描述统计表格里面的t 检验是什么意思?
-
Bland-Altman描述统计里面的t 检验,其原理为配对t 检验,检验的原假设是差值的平均值为0,即两种测量方法具有一致性,通常希望检验不能呈现出显著性,即接受原假设,论证两种测量方法具有一致性。
-
一致性检验的方法有哪些?
-
一致性检验是一种思想,其在于研究两种方法(或两个医生,也或者两次测量,或者两个医生)数据的一致性,其检验方法有很多种,比如组内相关系数ICC,Kappa系数, Kendall W协调系数,Bland-Altman图,甚至配对t 检验等均可。建议结合数据类型,以及研究者的在乎点进行选择使用即可,各方法操作可在医学研究/实验模块中找到。
-
