-
正交试验设计进行分析的方法包括两种,一种是极差分析(也称直观分析法),二是方差分析法。如果使用方差分析,可使用SPSSAU进阶方法里面的多因素方差,也或者通用方法里面的方差分析进行研究。
-
极差分析是一种直观式的分析方法,其也称作R法,通过计算R值(因素极差值)来判断因素的优劣情况,当然还可判断某因素时的最佳水平情况,从而得到最终组合。
-
特别提示:
-
极差分析是针对正交试验设计数据,比如使用SPSSAU医学/实验研究里面的正交设计数据得到正交表,进行试验得到试验数据后需要进行直观式分析。
-
极差分析案例
-
1、背景
当前有一项研究,研究大豆出油率分别与3个因素的关系情况,分别是萃取液,温度和处理时间。首先使用SPSSAU的正交设计得到正交表L9.3.4,总共进行9次试验收集完成试验数据后进行分析,希望找出3个因素时各水平的最佳大豆出油率组合。
水平 萃取液 温度 处理时间 1 10 20度 1.5小时 2 50 35度 2.5小时 3 90 50度 3.5小时 另外,本案例数据如下表:表格中水平数量使用数字表格,比如因子2(温度)里面的数字1表示20度,数字2表示35度。
试验编号 因子1(萃取液量) 因子2(温度) 因子3(处理时间) 大豆出油率(%) 1 1 1 1 0 2 1 2 3 16 3 1 3 2 21 4 2 1 3 14 5 2 2 2 49 6 2 3 1 29 7 3 1 2 1 8 3 2 1 19 9 3 3 3 45 -
2、理论
极差分析是一种直观式分析方法,一般我们希望先评价因素优劣,比如本案例中三个因素的优劣,评价标题是通过R值(因素极差值)进行评价;而具体水平的优劣可通过K avg值,即每个水平时试验数据的平均值,对于K avg值的大小即可得到水平优劣的对比。最终结合因素优劣和水平优劣,即可找出最佳试验组合。
-
特别提示:
-
极差分析时,涉及相关指标的计算说明如下:
-
K值:每因子每水平时 实验数据Y的 加和值
-
K avg值:每因子每水平时 实验数据Y的 平均值
-
最佳水平:每因子时,K avg值最大时对应的水平
-
R:每因子时,K avg值的最大值 减去 K avg值的最小值
-
水平数量:每因子时的水平数量
-
每水平重复数r:每个水平平均实验次数
-
折算系数d:每因子时,水平数量对应的折算系数d值
-
R’: 折算系数d * R * Sqrt(每水平重复数r)
-
如果是混合型正交表,R值(因素极差值)需要进行校正,即使用R’值,R’=折算系数d * R * Sqrt(每水平重复数r),其中折算系数d是结合水平数量查表得到,每水平重复数r指每水平平均实验次数。
-
-
3、操作
本例子中共有3个因素,分别是萃取液量,温度和处理时间,数据在EXCEL中整理好后上传后准备分析,放置分析项情况操作如下:
-
4、SPSSAU输出结果
SPSSAU共输出表格和图形,“极差分析表格”,列出各项指标,包括K值,K avg值,最佳水平,R值,水平数量和每水平重复数r,如果是混合型正交表还会提供折算系数d值和R’值(校正R值),各个指标的意义说明如下:
-
K值为某因素某水平时试验数据求和;
-
K avg值为对应的平均值;
-
最佳水平指某因子时最佳K avg值对应的水平编号;
-
R指因素的极差值,该值=某因素时,K avg最大值 减去 K avg最小值,可结合因素极差值对比各因素的优劣;
-
水平数量指某因素的水平数,每水平重复数r指水平的平均试验重复次数;
-
如果是混合型正交表,则会提供折算系数d(结合水平数量在折算系数表中找到)和R'值。
-
-
5、文字分析
极差分析表格 项 水平 因子1(萃取液量) 因子2(温度) 因子3(处理时间) K值 1 37.00 15.00 48.00 2 92.00 84.00 71.00 3 65.00 95.00 75.00 K avg值 1 12.33 5.00 16.00 2 30.67 28.00 23.67 3 21.67 31.67 25.00 最佳水平 2 3 3 R 18.33 26.67 9.00 水平数量 3 3 3 每水平重复数r 3.0 3.0 3.0 上表格为极差分析的结果,极差分析表格中可知:从3个因素来看,结合R值(因素极差值)的大小对比可知,因子2温度是最优因素,其次是因子1萃取液量,最后是因子3处理时间。因而3个因素的优劣排序为:因子2(温度)>因子1(萃取液量)>因子3(处理时间)。
具体结合各因子的最佳水平可知,因子1萃取液量时第2个水平即50时最优,因子2温度以第3个水平即50度最优,因子3处理时间以第3个水平即3.5小时最优。
综合上述分析可知:最优因子为温度。最优组合为“温度50度,萃取液量50,处理时间3。5小时”。
通过图形可直观查看如下:
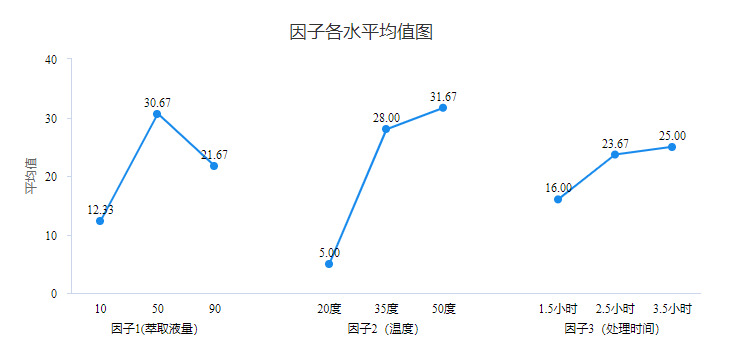
-
6、剖析
涉及以下几个关键点,分别如下:
-
极差分析是针对正交试验设计数据,比如使用SPSSAU医学/实验研究里面的正交设计数据得到正交表,进行试验得到试验数据后需要进行直观式分析。
-
如果是混合型正交表,R值(因素极差值)需要进行校正,即使用R’值,R’=折算系数d * R * Sqrt(每水平重复数r),其中折算系数d是结合水平数量查表得到,每水平重复数r指每水平平均实验次数。
-
正交设计数据时,可使用直观分析法即当前的极差分析,同时也可使用方差分析法进行研究(可使用SPSSAU进阶方法里面的多因素方差,也或者通用方法里面的方差分析进行研究)。
-
疑难解惑
-
极差分析数据格式提示?
-
极差分析时,上传数据的格式上一定需要为因子水平编号,比如1,2,3(即第几个水平编号),上传后使用数据处理->数据标签功能,标识数字代表的水平实际意义。具体数据格式可点击查看。
-
极差分析时试验数据越小越好?
-
默认情况下试验数据越大越好,如果试验数据越小越好,此时可下拉选择‘试验数据类型’参数为‘越小越好’即可。试验数据类型的变化,会对‘最佳水平’,R值及R’值有影响,其它指标值并无变化。
-
SPSSAU极差分析时试验数据类型‘越小越好’时的R值解读?
-
当试验数据类型‘越小越好’时,此时R值=最小值-最大值。因而依旧为R值越大越好。
