K近邻KNN模型
-
案例数据下载 下载
K近邻KNN(k-nearest neighbor)是一种简单易懂的机器学习算法,其原理是找出挨着自己最近的K个邻居,并且根据邻居的类别来确定自己的类别情况。比如K为5个,即找出挨着自己最近的5个邻居,5个邻居中有4个是‘富人’,那么自己也会被标签为‘富人’。此处涉及几个点,一是距离如何计算,二是K值如何选择,三是如何归类。接下来案例部分将具体进行说明。
除此之外,K近邻KNN模型与Kmeans有些类似,二者目的都是分类,但Kmeans是事先不知道数据如何分类,KNN事先已经知道如何分类,二者有时候可以匹配着使用,比如先使用kmeans得到聚类类别,然后使用KNN模型分析聚类效果情况等。
K近邻KNN模型案例
-
1、背景
K近邻模型依旧经典的‘鸢尾花分类数据集’进行案例演示,其数据集为150个样本,包括4个特征属性(4个自变量X),标签为鸢尾花卉类别,其分为3个类别分别是刚毛鸢尾花、变色鸢尾花和弗吉尼亚鸢尾花(下称A、B、C三类)。
-
2、理论
K近邻KNN模型的原理上示意如下图:
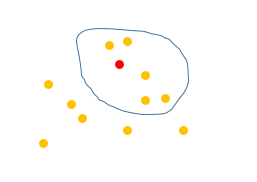
比如红色点,挨着其最近的5个点(K=5时)如上图,如果该5个点中多数均为A类,那么红色点就归为A类。需要注意的是,通常情况下K值为奇数,因为如果为偶数比如为6,那么3个为A类3个为B类,此时不好划分点的类别。
上述中关于挨的最近的距离,如何进行衡量呢?距离的计算方式非常多,比如欧式距离、曼哈顿距离等,通常情况下使用欧式距离,其计算公式如下:
比如有两行数据分别3列(即3个X,3个特征项),两行数据分别是(1,2,3)和(3,4,5),那么
另外关于K值的选择上,通常建议K介于3~20之间,且一般为奇数值,SPSSAU默认为5,如果说K值太大,容易出现‘过拟合’现象即结果看着很好但事实上不好;如果K值过小,容易出现拟合现象很糟糕(欠拟合)现象。实际使用时,可考虑分别设置不同的K值,然后对模型的优劣进行汇总和对比。
关于归类问题,上述比如K=5,挨的最近5个点中有3个(超过一半)为A类,那么该点就分为A类,此种分类方式为‘等比投票权’,即5个点的权重完全一致。但我们知道,挨的最近的5个点,其实都能计算出距离值,是否可根据距离值大小来加权判断呢?比如使用距离值的倒数,即1/距离值作为权重,如果距离值越大,权重就越小,并且综合计算来评估类别划分,此种方式叫‘距离反比投票权法’。关于类别划分参数,其叫‘样本投票权重’。
关于K近邻KNN模型时,通常涉及到以下参数值,如下:
参数 说明 参数值设置 邻近样本个数 K值,挨的最近邻居个数 默认5。可根据实际情况增减。 样本投票权重 两种分类依据方式 等比投票权:每个样本的投票权重一样;
距离反比投票权:样本距离的倒数作为权重,距离越近权重越高,反之越低。距离计算方法 用于计算样本点之间距离的方法 欧氏距离:默认,一般使用欧式距离即可。
曼哈顿距离:可选。邻近搜索方法 找出邻近K个值的时候使用的搜索方法。 全局搜索:蛮力实现,计算并搜索所有的样本点。
KD树:(KD tree)对训练集构造KD树,用KD树来搜索邻近样本点。
球树:(ball tree)对训练集构造球树,用球树来搜索邻近样本点。邻近样本个数K值,一般为奇数,并且常介于3~20之间,可设置不同的K值来对比不同模型的优劣。样本投票权重,默认是‘等比投票权’,可选为‘距离反比投票权’,建议K值较小时可考虑使用‘距离反比投票权’法。距离计算方法上,默认是欧式距离,可选曼哈顿距离,通常使用欧式距离即可。邻近搜索方法上,一种是全局搜索,比如100个样本,某个点分别先计算出该点离另外100个样本的距离,然后找出其中最小的K个,此种方式简单易懂,但是计算费资源,因而延伸出KD树和ball树两种优化算法。默认情况下系统会自动结合数据情况选择邻近搜索方法,研究者也可自行选择。
-
3、操作
本例子操作如下:
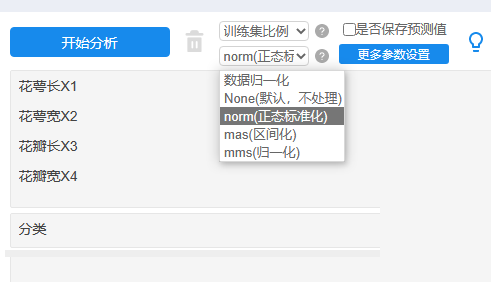
训练集比例默认选择为:0.8即80%(150*0.8=120个样本)进行训练K近邻KNN模型,余下20%即30个样本(测试数据)用于模型的验证。需要注意的是,多数情况下,会首先对数据进行标准化处理,处理方式一般使用为正态标准化,此处理目的是让数据保持一致性量纲。当然也可使用其它的量纲方式,比如区间化,归一化等。
接着对参数设置如下:

邻近样本个数K值默认为5,样本投票权重方式为‘等比投票权’,邻近搜索方法自动让系统选择,距离计算方式为‘欧氏距离’法。
-
4、SPSSAU输出结果
SPSSAU共输出5项结果,依次为基本信息汇总,训练集或测试集模型评估结果,测试集结果混淆矩阵,模型汇总表和模型代码,如下说明:
项 说明 基本信息汇总 因变量Y(标签项)分类数据分布情况等 训练集或测试集模型评估结果 分析训练集和测试集数据的模型效果评估,非常重要 测试集结果混淆矩阵 测试集数据的进一步效果评估,非常重要 模型汇总表 模型参数及评估汇总表格 模型代码 模型构建的核心python代码 上述表格中,基本信息汇总表格展示因变量Y的分类数据分布情况,接着展示训练集和测试集效果情况,并且单独提供测试集数据混淆判断矩阵,进一步分析测试数据的正确效果等,模型汇总表格展示整体模型参数情况,并且提供sklean进行KNN模型构建的核心代码。
-
5、文字分析
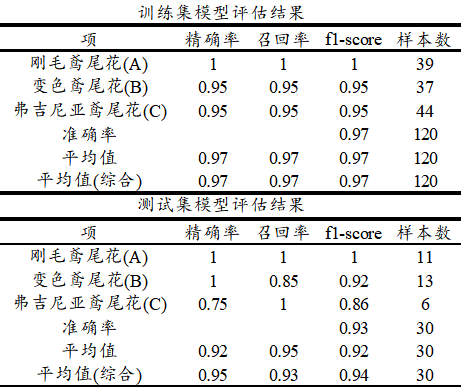
上表格中分别针对训练集和测试集,提供四个评估指标,分别是精确率、召回率、f1-scrore、准确率,以及平均指标和样本量指标等,如下表格说明:
项 说明 精确率 比如:预测为A类时,事实上是A类的比例,越大越好 召回率 比如:事实上是A类时,预测为A类的比例,越大越好 F1-score 精确率和召回率的调和平均数,越大越好,一般使用此指标较多 准确率 整体上全部数据预测准确的比例情况,越大越好,仅1个数字 平均值 对应指标的平均值,越大越好 平均值(综合) 对应指标的加权平均值(考虑样本量情况下) 样本量 各类别的样本量情况 一般来说,f1-score指标值最适合,因为其综合精确率和召回率两个指标,并且可查看其平均值(综合)指标,本案例为0.97,并且测试数据的表现上为0.94,意味着评估效果好,当前的KNN模型(基于K值为5时)表现良好。当然也可以更新K值个数,比如设置为7,重新运行结果并且对比选择最优模型。事实上当前设置K=7时,训练集的f1-scroe由0.97上升到0.98有点提升,但这并不重要,因为当K值更大时,理论上模型就会变的更好,反倒训练集时太好了反倒有‘过拟合’现象,因而应该更多关注于测试集数据,测试集数据的f1-score值为0.94,说明测试集表现基本一致(测试集数据的拟合表现非常关键)。
进一步地,可查看测试数据的‘混淆矩阵’,即模型预测和事实情况的交叉集合,如下图:
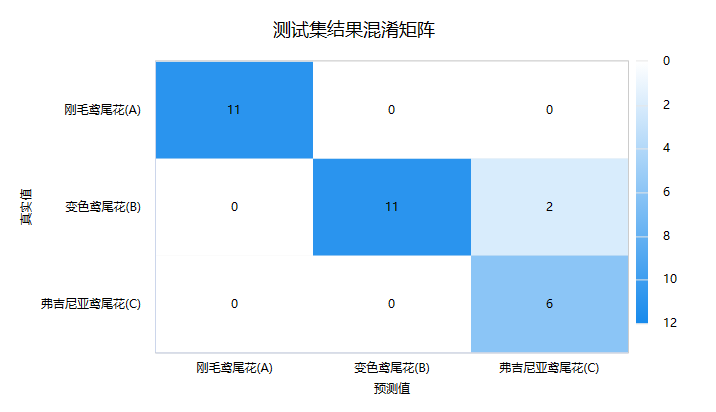
‘混淆矩阵’时,右下三角对角线的值越大越好,其表示预测值和真实值完全一致。上图中B类时有2个测试数据被预测为C类,错误率较低。
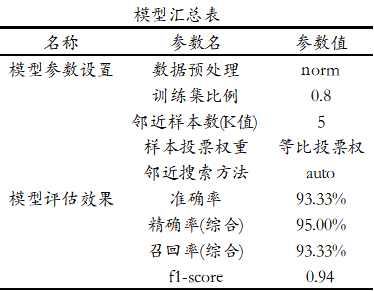
最后针对模型汇总表,其展示构建K近邻KNN的各项参数设置,包括针对数据进行标准化正态处理,参数值为norm,训练集占比和K值设置等。最后,SPSSAU输出使用python中slearn包构建本次K近邻KNN模型的核心代码如下:
model = KNeighborsClassifier(n_neighbors=5, weights=uniform, algorithm=auto, p=2)
model.fit(x_train, y_train)
-
6、剖析
涉及以下几个关键点,分别如下:
-
K近邻KNN模型时是否需要标准化处理?
-
一般建议是进行标准化处理,通常使用正态标准化处理方式即可,当然也可使用比如归一化处理等,其目的是处理特征的单位量纲问题,试想身高为1.8与体重为50公斤,这单位不同计算距离时会有严重影响。
-
训练集比例应该选择多少?
-
如果数据量很大,比如1万,那么训练集比例可以较高比如0.9,如果数据量较小,此时训练集比例选择较小预留出较多数据进行测试即可。
-
保存预测值
-
保存预测值时,SPSSAU会新生成一个标题用于存储模型预测的类别信息,其数字的意义与模型中标签项(因变量Y)的数字保持一致意义。
-
SPSSAU进行K近邻KNN模型构建时,自变量X(特征项)中包括定类数据如何处理?
-
K近邻KNN模型时,如果有定类数据,建议对其哑变量处理后放入,关于哑变量可 点击查看。
-
疑难解惑
-
SPSSAU机器学习如何进行预测?
-
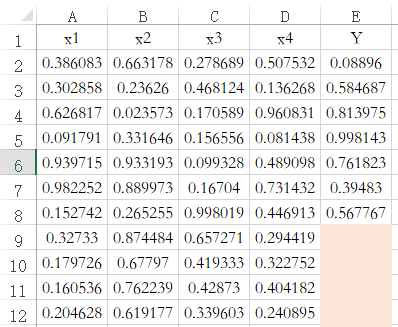
SPSSAU中默认带有数据预测功能,当特征项X有完整数据,但标签项(因变量Y)没有数据时,此时‘保存预测值’,SPSSAU会默认对此种情况进行预测。如下图中的编号9到12共4行数据,其只有X没有Y,那么保存预测值时,默认对该4行数据进行预测。机器学习的各方法(包括决策树/随机森林/KNN/贝叶斯/支持向量机和神经网络等)均遵从此规则。
-
SPSSAU机器学习中量纲归一化处理的具体规则情况?
-
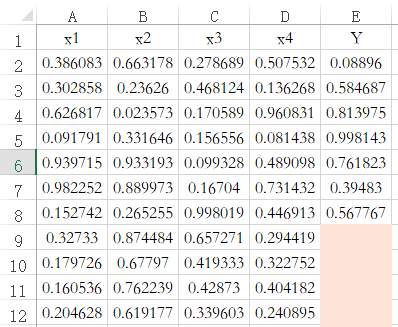
SPSSAU中,机器学习时均具有归一化参数值,并提供正态标准化/区间化/归一化等方式。其原理是针对具有完整数据的特征项X分别进行处理。比如下图中是针对编号为2~12共计11项的4个X分别进行处理。
-
机器学习中分类任务和回归任务的区别是什么?
-
机器学习包括分类任务和回归任务,当标签项(因变量Y)为类别数据时,其为分类任务,比如研究X对于“贷款是否逾期”的预测作用,“是否逾期”这个分类数据,因而此时此为分类任务。如果因变量Y为定量数据,比如研究X对于“贷款金额”的预测作用,“贷款金额”为定量数据,因而为回归任务。决策树/随机森林/支持向量机和神经网络等时,SPSSAU默认会对因变量Y进行识别,并且自动选择分类任务或者回归任务。当然研究者可以在“更多参数设置”处进行选择设置。另外,KNN和贝叶斯这两项仅提供分类任务。
-
机器学习时提示‘分类数据必须为整数’?
-
机器学习包括分类任务和回归任务,如果是定量数据Y进行分类任务,此时系统会提示“分类数据必须为整数”。决策树/随机森林/支持向量机和神经网络等时,可通过“更多参数设置”处进行选择设置,以及KNN和贝叶斯这两项仅提供分类任务。
-
机器学习算法时保存数据集标识的意思是什么?
-
选择‘保存数据集标识’后,SPSSAU会新生成一个标题,用于标识模型构建时训练集或测试集,使用数字1表示训练集,数字2表示测试集。如果后续分析时(比如绘制ROC曲线)只针对训练集,那么使用筛选样本功能,筛选出训练集后分析即可。
-
如何将多个机器学习模型数据绘制ROC曲线?
-
如果有多个机器学习模型后,需要对比模型优劣情况。建议按下述步骤进行。
-
第1步:每个机器学习模型最后一次构建后,选中‘保存预测信息’,系统会生成类别的预测概率;
-
第2步:将多个机器学习模型的某类别的预测概率值一并纳入作为X,以及将Y作为Y,进行ROC曲线【注意,放入的是某个类别的预测概率值】;
-
第3步:设置ROC曲线时对应的分割点,需要注意的是,分割点一定要设置为放入的对应类别时预测概率值对应的数字。
-
需要提示的是:预测概率是指某类别的预测概率值,二分类时只有两个数字,比如是和否(数字1和数字0表示),那么‘是’对应的预测概率值即为模型预测出‘是’的概率,‘是’和‘否’的概率加和一定为1。
-
机器学习算法中保存预测信息具体是什么意思?
-
如果选中保存预测信息,并且为分类任务时,SPSSAU会新生成两项标题,分别是预测类别和预测概率。预测类别是指最终预测出来Y的类别,预测概率是指预测出Y的每个类别对应的概率情况;事实上某个类别的预测概率相对最大时,此时预测类别就为该类别(比如Y有A/B/C共3个类别,某样本时3个类别的预测概率分别是0.4,0.5,0.1),那么预测类别则为B类别。
-
预测类别标题名称类似为‘NeutralNetwork_Prediction_****’,以及预测属于每个类别概率标题名类似‘NeutralNetwork_Prediction_probability_****’。
-
保存预测信息后,可进一步使用预测概率进行其它的分析或者处理,比如绘制ROC曲线等。