在时间序列进行预测时, ARIMA可用于单一变量(比如GDP增长率)的预测,如果需要同时考虑几个变量的预测时(比如GDP增长率、失业率、储蓄率),此时可考虑分别针对研究变量进行,即多次重复进行。通常情况下同一系统的几个研究变量之间均有着相互依旧关系,因而为更好的利用各变量的此类关系,此时可以使用VAR模型(Vector autoregressive model)进行多变量预测。VAR模型的构建流程较为复杂,如下图所述:
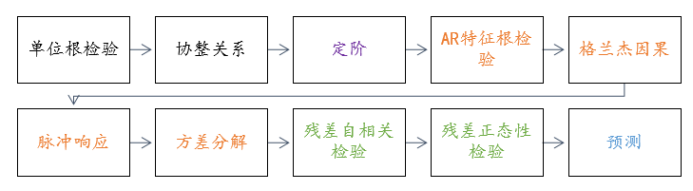
通常情况下,VAR模型需要满足单位根检验,如果没有单位根则直接构建VAR模型即可,如果研究变量有单位根,则说明不适合进行VAR模型构建,但是如果有单位根且满足同阶单整,此时说明VAR模型构建是适合的,与此同时研究变量满足协整关系也是一种常见的前提条件。
VAR模型构建时,通常包括定阶这一步骤,即选择适合的滞后阶数。VAR模型构建完成后,接着还需要对模型的有效性进行分析,通常是针对AR特征根图进行分析。另外,理论上VAR模型的残差还满足满足正态性,并且通过自相关检验等,但通常对此类检验的关注度相对较少。
VAR模型构建之后,通常需要进行比如格兰杰困果检验,脉冲响应和方差分析,用于进一步分析研究变量之间的相互作用依存关系情况。
最后,可得到模型的预测数据,满足模型预测目的。
-
特别提示:
-
如果是使用VAR模型判断平稳性,其为直观图示法,带有一定的主观性,反之使用比如SPSSAU的ADF检验平稳性,二者有可能出现不同的结论。
VAR模型案例
-
1、背景
当前有一项美国宏观联邦基金利率、通货膨胀率和失业率的数据,数据日期从1960年第1季度到2012年第1季度,单位为季度,共计209个数据。现希望查看,该3项数据具有具有稳定性,便于后续的分析使用。部分数据如下图所示:
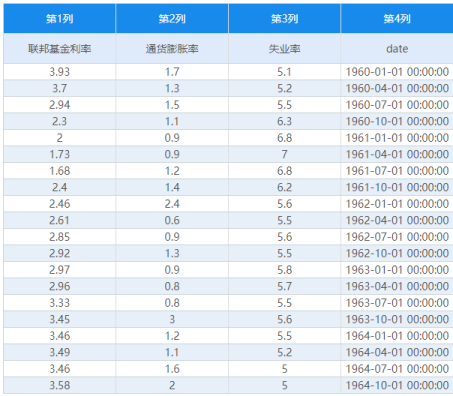
-
2、理论
VAR模型有着较为复杂的分析流程步骤,具体可参考下图和表格所述。下述分析步骤和流程仅供参考使用,实际研究中可能仅需要其中一部分的分析即可。比如很多时候并不需要关注残差自相关检验和残差正态性检验,也或者有时对格兰杰因果检验关注度较少等,具体以研究者实际研究情况为准即可。

项 说明 单位根检验 模型要求研究变量保持平稳性,可使用单位根检验检验平稳性性,也或者使用时序图亦可。 协整关系 协整关系研究系统的长期稳定性情况,通常有两种方法,分别是Johansen法和Engle-Granger法研究协整关系。可使用SPSSAU –> coint协整进行分析。 定阶 进行VAR模型时,需要针对滞后阶数进行选择,SPSSAU可自动识别最佳滞后阶数。 AR特征根检验 AR特征根检验可用于分析VAR模型系数稳定有效性情况。 格兰杰因果 研究变量间的‘相互影响关系’情况。 脉冲响应 其用于研究变量间的动态影响关系情况。 方差分解 其用于研究变量间的影响比例情况。 残差自相关检验 研究模型残差的自相关性情况。 残差正态性检验 研究模型残差的正态性情况。 预测 得到模型的预测值,用于研究使用。 -
1.关于单位根检验。
-
如果变量无单位根,则满足前提条件直接进行VAR模型即可(一般不需要再进行协整关系研究);
-
如果变量有单位根,可对变量差分,如果同阶单整,则可进行下一步协整关系分析;
-
如果变量有单位根,且变量差分后不满足同阶单整,则不满足前提条件无法进行VAR模型。
-
2.关于协整关系。
-
SPSSAU计量研究模块中提供协整检验,并且提供Johansen法和Engle-Granger法两种选择使用。
-
如果原始序列变量直接没有单位根(或图示非常平稳),直接进行VAR模型即可。
-
如果原始序列有单位根且满足同阶单整,此时需要满足协整关系,即系统有着长期稳定性后,此时才可进行VAR模型构建。
-
3.关于定阶。
-
如果满足协整关系后,则意味着可进行VAR模型构建;
-
VAR模型时需要进行阶数确定,此过程可让SPSSAU自动选择,也可手工构建多次模型,结合AIC/SC等信息准则指标越小越优原则,找到最佳滞后阶数,然后手工设置滞后阶数。
-
4.关于AR特征根检验。
-
VAR模型构建后,模型参数的稳定性如何,可通过AR特征根进行检验,如果点全部在单位圆内,则意味着通过特征根检验,模型参数具有稳定性。
-
5.关于格兰杰因果。
-
VAR模型构建之后,也可进行格兰杰困果检验,进一步分析变量之间的相关依存关系情况。
-
6.关于脉冲响应。
-
脉冲响应用于研究变量之间的动态影响关系情况,通常在VAR模型之后均需要进一步分析使用,SPSSAU默认使用正交化脉冲响应。
-
7.关于方差分解。
-
方差分解用于研究变量之间影响关系的解释比例情况,通常在VAR模型之后均需要进一步分析使用。
-
8.关于残差自相关检验。
-
模型构建后残差自相关性情况如何,可查看SPSSAU输出残差自相关检验表格,具体为 Portmanteau检验,通常情况下,VAR模型构建时对残差自相关性的关注度相对较低。
-
9.关于残差正态性检验。
-
模型构建后残差是否满足正态性,可查看SPSSASU输出残差自相关检验表格,通常情况下,VAR模型构建时对残差自相关性的关注度相对较低。
-
10.关于预测。
-
VAR模型的重要目的在于进行预测,SPSSAU默认提供向后12期的预测数据,当然也可自行进行设置预测期数。
-
-
3、操作
本例子操作截图如下,放入3个分析项(并且分析项需要注意放入顺序,便于后续分析使用),SPSSAU‘Trend类型’默认为常数,滞后阶数lags上默认是自动定阶,预测期数设置为40,即往后预期40期数据。
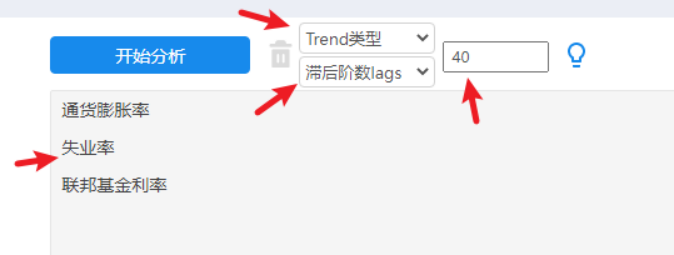
关于‘Trend类型’说明:本案例的3个数据并没有明显的趋势而且均值也不接近于0,因而选择默认的常数类型即可,绝大多数时候均应该使用常数类型。如果说研究变量的均值基本上接近于0,可以考虑使用‘None’类型,如果说研究变量有着较为明显的趋势项,此时可考虑使用‘线性趋势T’。具体更多说明可见本文档末尾的疑难解惑说明。
滞后阶数让系统自动定阶,当然研究者也可以自主设置阶数,具体设置原则建议结合专业知识,或者信息准则越小越好进行判断,多次构建模型对比不同滞后阶数时信息准则的大小,选择出信息准则最小对应的滞后阶数模型即可。
预测基数上,本研究设置为40,即向后预测40个季度的数据。
-
4、SPSSAU输出结果
SPSSAU分别8类表格,以及4种图形,分别如下说明。
输出项 说明 基本参数表格 展示基本的模型参数设置结果 自动定阶 展示SPSSAU自动定阶结果表格,如果手工设置滞后阶数,此时不会输出该表格 VAR模型结果 展示模型结果,包括参数值和信息准则等结果 Inverse Roots of AR Characteristic Polynomial 展示AR特征根单位圆 脉冲响应图 展示脉冲响应图,并且可下拉选择查看不同变量时的脉冲响应图 脉冲响应表格 展示脉冲响应表格,并且可下拉选择查看不同变量时的脉冲响应表格 方差分解图 展示方差分解图,并且可下拉选择查看不同变量时的方差分解图 方差分解表格 展示方差分解图表格,并且可下拉选择查看不同变量时的方差分解表格 模型预测表格 展示向后预测的具体数字 模型预测图 图形展示各后预测数据 残差正态性检验表格 展示模型残差正态性检验结果 残差自相关检验表格 展示模型自相关性检验结果 -
5、文字分析
通常情况下VAR模型构建之前需要查看研究变量的稳定性,可通过时序图或者单位根检验进行分析,如果存在单位根或者图示出来明显不平稳,则不能构建VAR模型。如果说差分后数据平稳(即同阶单整),也可以进行VAR模型构建,本次研究数据本身不平稳,但是1阶差分后的数据平稳即满足同阶单整前提。因而可以构建VAR模型,3个研究项进行1阶差分后的时序图如下图所示:
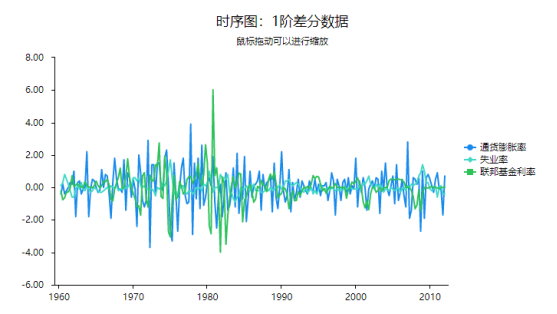
与此同时VAR模型之前一般还可进行协整检验,本次构建模型数据进行‘Johansen协整检验’后显示具有协整关系,即说明模型参数值具有长期稳定性,也即说明模型可靠,由于coint协整检验在SPSSAU中隶属于单独一个研究方法(其并不隶属于VAR模型),研究者可单独进行分析处理即可;除此之外,VAR模型分析后通常还需要研究格兰杰因果关系,其需要单独使用SPSSAU的格兰杰因果分析方法进行研究即可。
接下来逐一描述VAR模型输入的表格及图形结果等,如下:

上表格展示VAR模型参数设置情况,包括趋势类型、滞后阶数情况和预期期数;其仅为模型设置的参数展示,并不特别分析意义。本次模型时自动定阶为2阶,即构建VAR(2)模型。
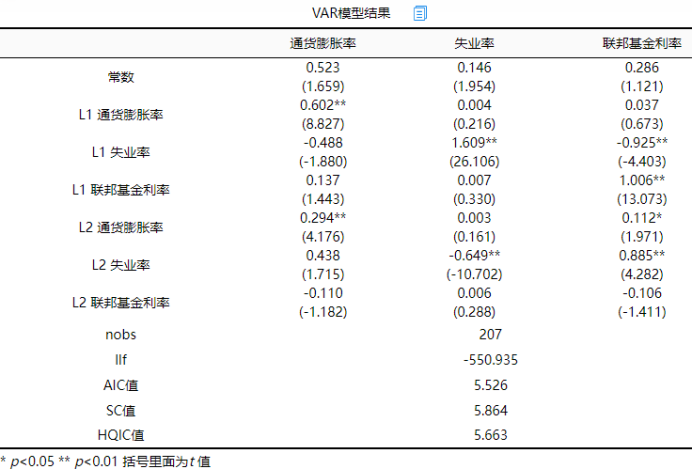
上表格展示VAR模型参数结果值;通常情况下上表格中值的意味相对较小,如果需要分析,首先查看是否显著,如果呈现出显著性后再分析影响关系情况,通常情况下并不需要分析,本次也并不对上述参数进行分析,其仅作展示使用。另外,上表格中还提供llf似然值,以及AIC、SC和HQIC这3个信息准则值。
一般情况下,如果需要对比模型优劣,可通过对比3个信息准则值的大小(越小越优)来进行模型综合选择使用。
-
特别提示:
-
由于本次滞后阶数为2阶,因而本身有209个数据,但上表格中显示为207;
-
由于本次滞后阶数为2阶,因而参数中L1代表滞后1阶,L2代表滞后2阶。
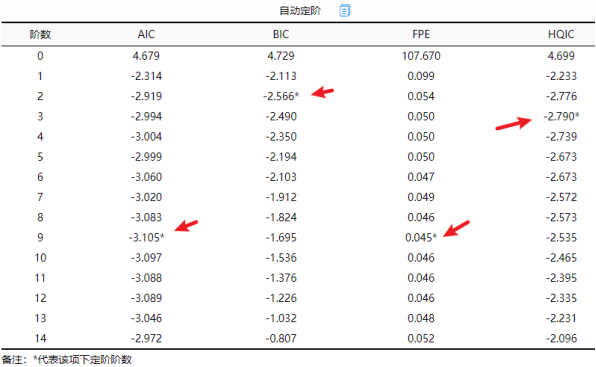
上表格展示自动定阶的过程值,SPSSAU自动定阶的原则为信息准则值越小越优,共有提供4个指标值,分别是AIC、BIC、FPE和HQIC,如果按照AIC准则时应该以9阶为准, BIC准则时应该以2阶为准, FPE时应该以9阶为准, HQIC准则时应该以3阶为准。4个指标值中最小值为2阶,因而SPSSAU最终以2阶为准构建VAR模型。
-
特别提示:
-
一般情况下,滞后阶数越小时,可利用的样本信息越高,并且模型相对越简单,因而一般使用尽可能小的滞后阶数,建议直接使用SPSSAU的自动定阶建议值即可;
-
上述中共有4个判断指标,理论上研究者可使用任意其中1个作为标准,当然研究者也可分别设置不同的滞后阶数,然后对比不同模型信息准则值来判断哪个模型更优(根据信息准则越小越优标准)。
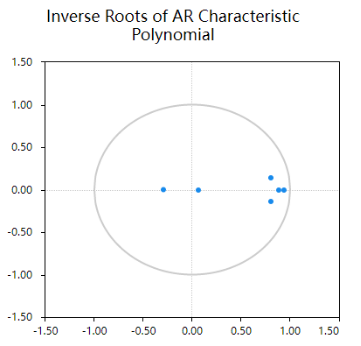
VAR模型构建后,可以通过AR根图判断VAR模型的稳定性;如果所有特征值均在单位圆内,即所有点均在圆内,此时说明模型具有稳定性;如果出现特征根在单位圆之外,意味着模型可能不具有长期持续稳定性。
AR根图是模型构建后模型质量的判断,一般情况需要查看此项,上图可以看到,所有特征根值均在单位圆之内,意味着构建的VAR模型稳定性较好,也即说明本次模型构建良好。
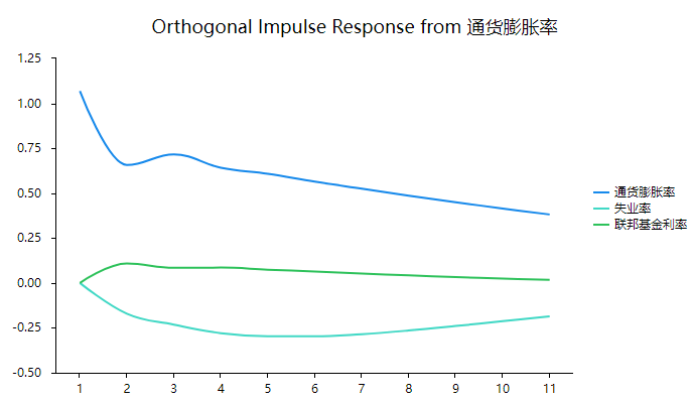
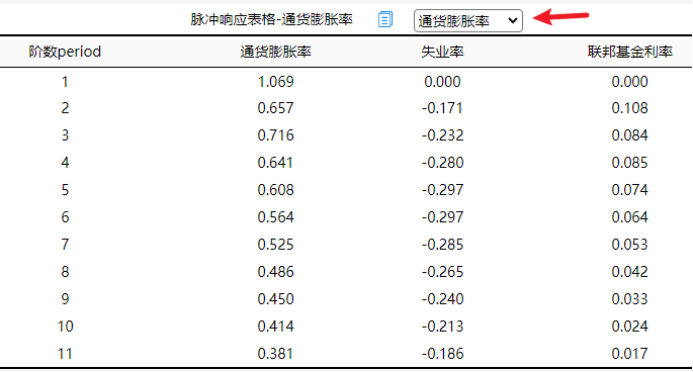
上图展示正交化脉冲响应图,并且下表格有具体数据。正交化脉冲响应图展示某变量冲击对该变量自身或其它变量产生的动态影响情况;如果大于0则为正向冲击,反之小于0则为负向冲击,绝对值越大意味着冲击越大,值越接近于0意味着冲击越小。
从上图可以看到:针对‘通货膨胀率’冲击变量,通货膨胀率首先对自身产生正向的冲击,然后冲击力度逐渐平稳减小,但一直均有着冲击且冲击力度较大。通货膨胀率对于失业率的冲击上,其先会产生负向抑制作用,前4期时此种负向冲击作用逐渐加强,但从第5期开始,负向冲击作用逐渐减弱并且趋于平稳,一直均为负向冲击。通货膨胀率对于联邦基金利率的冲击上,一直均有着微弱的正向冲击作用,但作用力度非常有限。
除此之外,关于失业率对于3个研究变量的脉冲响应分析表格或图,也或者联邦基金利率对于3个研究 变量的脉冲响应分析表格或图。可通过下拉选择进行切换展示分析。
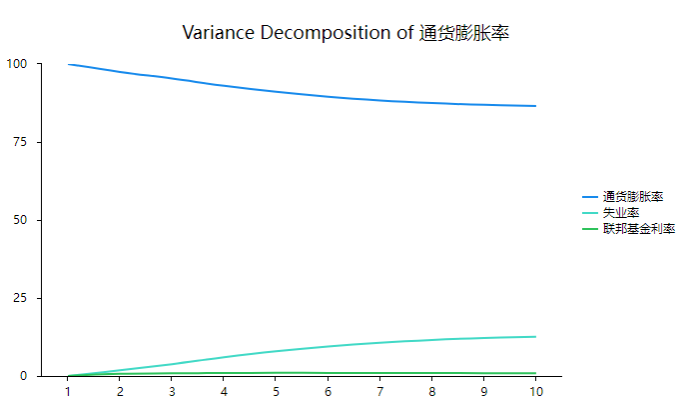
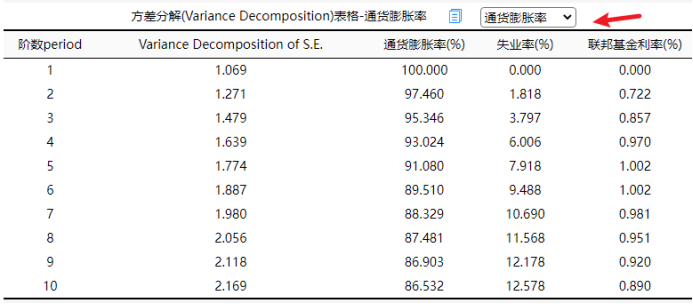
上图展示预测误差方差分解情况,以及上表格展示具体数据;方差分解fevd目的在于分析变量影响比例情况;方差分解图的横坐标为阶数,纵坐标为方差分解值,其可用于反馈随着滞后阶数变化时方差分解变化情况;方差分解值越大意味着影响比例越大,方差分解值接近于0时意味着影响甚微;
从上图可以看到,通货膨胀率对于自身的方差分解率非常高,基本上均大于85%,也即说明通货膨胀率对于自身的解释力度非常强非常相对较为平稳。对于失业率而言,通货膨胀率对其解释力度有限,基本上均低于10%,但是解释力度呈现出逐渐加大的趋势性,也即说明通货膨胀率对于失业率的影响是具有连续稳定的解释作用,并且随着时间变化,解释作用会逐步提高。最后,通货膨胀率对于联邦基金利率的方差分解来看,其分解力度非常有限,基本上均接近于0,也即说明通货膨胀率对于联邦基金利率的变化解释力度很小。
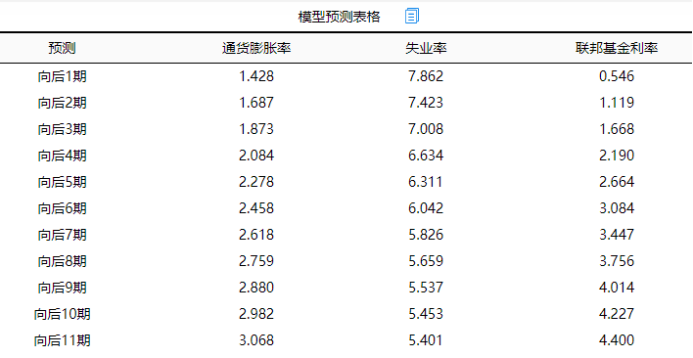
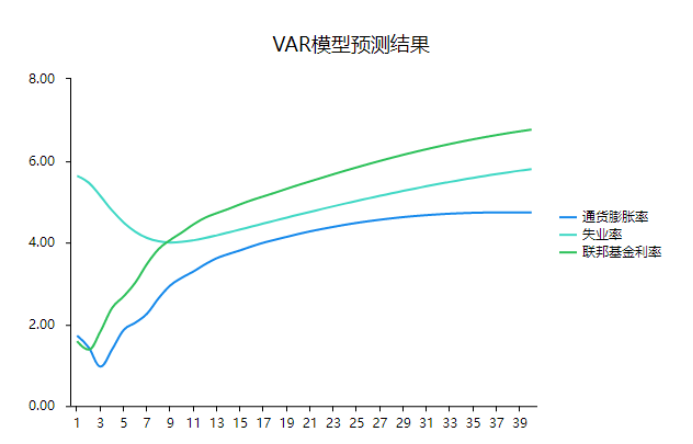
上表格展示模型预测结果,本次案例设置为40期(篇幅限制,上表格中仅11期),下图可直观查看模型预期结果数据,均为向后预测数据。

上表格展示残差正态性检验结果;理论上VAR模型需要满足残差正态性要求,但多数情况下对其关注度相对较小。上表格展示为最终联合性正态检验(χ2=1126.599,p 值=0.000<0.05),即意味着拒绝原假定,即说明模型没有通过正态性检验。但本研究暂不关注此指标。

上表格展示Portmanteau自相关检验结果;理论上VAR模型需要满足残差无自相关性要求,但多数情况下对其关注度相对较小。上表格展示检验(χ2=42.667,p 值=0.000<0.05),即意味着拒绝原假定,即说明模型没有通过自相关性检验。但本研究暂不关注此指标。
-
-
6、剖析
-
涉及以下几个关键点,分别如下:
-
VAR模型前通常还需要进行单位根检验(或者查看时序图)、协整检验,并且在模型后通常还需要查看格兰杰因果检验,该4项可通过SPSSAU的其它单独分析按钮进行分析使用。
-
如果VAR模型前研究变量有单位根,并且不满足同阶单整,通常不建议使用VAR模型;如果研究变量无单位根(或者时序图展示基本平稳),也或者有单位根但是满足同阶单整,那么此时可直接使用VAR模型。
-
VAR模型有着较多的前提条件,并且模型分析之后还有较多检验(比如正态性检验、自相关性检验等),一般VAR模型满足前提条件(无单位根或同阶单整,以及满足协整关系)即可,对于模型后的检验关注度相对较少。
-
最优滞后阶数设置上,建议阶数越小越好,结合SPSSAU自动定阶表格进行决定,如果需要对比模型优劣,通常可使用模型输出的信息准则指标进行综合对比选择即可。
-
疑难解惑
-
如果时间序列一阶单整和二阶单整,并且其它序列是二阶单整,是否可进行VAR模型构建?
-
如果时间序列经过一次差分变成平稳,则称原序列是1阶单整,记为I(1)。如果时间序列经过d次差分后变成平稳序列,则称原序列是d阶单整序列,记为I(d)。同阶单整是指两个或多个时间序列同为d阶单整。因而说明为2阶单整即I(2),此时如果原始序列通过协整检验,那么就可以进行VAR模型构建。
-
VAR模型时‘Trend类型’如何选择类型?
-
VAR模型时,SPSSAU共有三种类型可以选择,分别是截距(即常数),截距和趋势(即线性),无。其常见选择标准有两种,分别是‘主观判断法’和‘信息准则判断法’。
-
关于‘主观判断法’,说明如下表:
-
Trend类型 说明 常数c(默认) 如果序列均值明显不为0且也没有明显的长期趋势,则为常数。绝大多数情况下均应该默认为常数项即可。 线性趋势T 如果序列均值明显不为0且有明显长期趋势,则为‘截距和趋势’。类似GDP一般应包括趋势,比如利率/汇率等一般不应该有时间趋势。建议可通过时序图查看,是否有长期变化趋势,如果有则有趋势,反之则无趋势。 None 序列均值接近为0且也没有长期趋势,则为无。 -
关于‘信息准则判断法’,说明如下:
-
可结合SPSSAU输出的信息准则比如AIC值判断,比如分别使用3种类型得到3个不同的AIC值,然后对比找到AIC值最小时对应的类型使用即可。
-
如果同阶单整时,是否可以不进行格兰杰检验?
-
VAR模型时,如果原始序列平稳此时不需要进行协整检验,直接进行VAR模型分析即可,并且可进行格兰杰因果检验。如果出现原始序列不平稳且满足同阶单整(且通过协整检验),此时是否进行格兰杰检验并没有固定要求,此时如果要进行格兰杰检验,通常应该以差分后的序列数据进行,而非原始不平稳序列数据。
