TSLS是用于解决内生性问题的一种方法,除TSLS外还可使用GMM估计。内生变量是指与误差项相关的解释变量。对应还有一个术语叫‘外生变量’,其指与误差项不相关的解释变量。产生内生性的原因通常在三类,分别说明如下:
| 内生性原因 | 说明 |
|---|---|
| 遗漏变量 | 比如研究工资的影响因素时,解释变量纳入受教育年限,但个人能力未被纳入 |
| 变量有测量误差 | 比如使用成绩来测量IQ值 |
| 双向因果关系 | 比如受教育年限影响工资,工资反过来影响受教育年限 |
内生性问题的判断上,通常是使用Durbin-Wu-Hausman检验(SPSSAU在两阶段最小二乘回归结果中默认输出),当然很多时候会结合自身理论知识和直观专业性判断是否存在内生性问题。如果假定存在内生性问题时,直接使用两阶段最小二乘回归或者GMM估计即可。一般不建议完全依照检验进行判断是否存在内生性,结合检验和专业理论知识综合判断较为可取。
内生性问题的解决上,通常使用工具变量法,其基本思想在于选取这样一类变量(工具变量),它们的特征为:工具变量与内生变量有着相关(如果相关性很低则称为弱工具变量),但是工具变量与被解释变量基本没有相关关系。寻找适合的工具变量是一件困难的事情,解决内生性问题时,大量的工作用于寻找适合的工具变量。
关于引入工具变量的个数上,有如下说明:
| 项 | 说明 | Durbin-Wu-Hausman | 过度识别检验 |
|---|---|---|---|
| 过度识别 | 工具变量个数>内生变量个数 | 有 | 有 |
| 恰好识别 | 工具变量个数=内生变量个数 | 有 | 有 |
| 不可识别 | 工具变量个数<内生变量个数 | - | - |
过度识别和恰好识别是可以接受的,但不可识别这种情况无法进行建模,似想用一个工具变量去标识两个内生变量,这是不可以的。另需要提示,如果是恰好识别状态下是无法进行Durbin-Wu-Hausman检验。
工具变量引入时,有时还需要对工具变量外生性进行检验(过度识别检验),针对工具变量外生性检验上,SPSSAU默认提供Sargan检验和Basmann检验。特别提示,只有过度识别时才会输出此两个检验指标。
关于两阶段最小二乘法的原理上,其将估计分成两个步骤(阶段)回归。如下表格说明:
| 阶段 | 说明 | 目标 |
|---|---|---|
| 第一阶段 | 将内生变量与工具变量,外生变量进行回归 | 得到预测值Prediction(其目的在于替换内生变量) |
| 第二阶段 | 将被解释变量与Prediction,外生变量进行回归 | 得到最终结果 |
第一阶段回归结果为中间过程值,SPSSAU默认没有输出;第二阶段回归结果为最终结果值。
-
特别提示
-
内生性问题涉及以下几点,分别是内生变量判断(Durbin-Wu-Hausman检验和理论判断),内生性问题的解决(两阶段最小二乘回归TSLS或GMM),工具变量引入后过度识别检验(Sargan检验和Basmann检验)等。
-
如果在理论上认为可能某解释变量可能为内生变量,那么直接进行TSLS回归即可。
两阶段最小二乘回归案例
-
1、背景
本案例引入Mincer(1958)关于工资与受教育年限研究的数据。案例数据中包括以下信息,如下表格:
编号 名称 说明 类型 1 是否美国南方(1为南方) 数字1代表美国南方城市,数字0代表不是南方城市 - 2 婚姻(已婚为1) 数字1代表已婚状态,数字0代表未婚状态 外生变量 3 是否大城市(1为大城市) 数字1代表大城市,数字0代表不是大城市 外生变量 4 母亲受教育年限 工具变量 5 iq智商 - 6 成绩 工具变量 7 年龄 - 8 受教育年限 内生变量 9 工龄 - 10 当前单位工作年限 外生变量 11 Ln工资 工资的对数值 被解释变量 12 工资 - 数据共有12项,其中编号为1,5,7,8,12共五项并不在考虑范畴。
本案例研究‘受教育年限’对于‘Ln工资’的影响。明显的,从理论上可能出现‘双向因果关系’即‘受教育年限’很可能是内生变量。那么可考虑使用‘母亲受教育年限’和‘成绩’这两项数据作为工具变量。同时研究时纳入3个外生变量,分别是‘婚姻’,‘是否大城市‘和’当前单位工作年限’。使用两阶段最小二乘TSLS回归进行解决内生性问题。
本案例研究时,工具变量为2个,内生变量为1个,因而为过度识别,可以正常进行TSLS回归。
-
2、理论
两阶段最小二乘回归,其内部原理上共分为两次回归。第一次回归将内生变量与工具变量,外生变量进行回归,并且得到回归预测值Prediction;第二次回归将被解释变量与Prediction,外生变量进行回归,得到最终模型结果。第一次回归为中间过程值,SPSSAU并没有输出,如果有需要可自行使用线性回归或OLS回归进行即可。
-
关于内生性的检验Durbin-Wu-Hausman检验,其用于检验是否真的为内生变量;如果说检验不通过(接受原假设),那么说明没有内生变量存在,可直接使用OLS回归即可。当然即使没有内生性,一般也可以使用TSLS回归,没有内生性问题时,OLS回归和TSLS回归结论通常一致;
-
关于过度识别检验上,SPSSAU提供Sargan检验和Basmann检验(使用任意其一即可),原理上此过度识别检验仅在‘过度识别’时才会输出,即工具变量个数>内生变量个数时,才会输出。
-
-
3、操作
本案例分别将被解释变量,内生变量,工具变量和外生变量纳入对应的模型框中,如下:
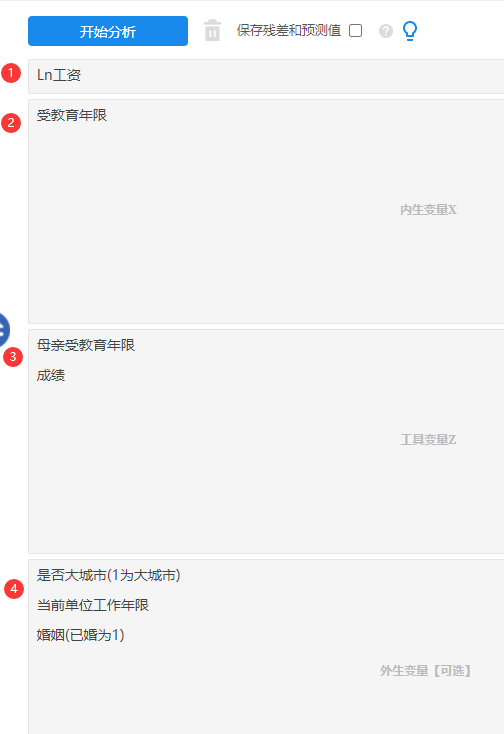
-
4、SPSSAU输出结果
SPSSAU共输出6类表格,分别是研究变量类型表格,2sls模型分析结果表格,2sls模型分析结果-简化格式表格,模型汇总(中间过程)表格,Durbin-Wu-Hausman test外生性检验(test of exogeneity)和过度识别检验(overidentifying restrictions)。说明如下:
表格名称 说明 研究变量类型表格 变量类型汇总表格 2sls模型分析结果表格 模型结果表格 2sls模型分析结果-简化格式表格 模型分析结果的简化格式表格 模型汇总(中间过程)表格 输出一般性指标比如R值 Durbin-Wu-Hausman test外生性检验(test of exogeneity) 是否存在内生变量检验 过度识别检验(overidentifying restrictions) 工具变量是否外生性检验表格,如果是‘恰好识别’则不会有此表格 -
5、文字分析
研究变量类型 类型 名称 被解释变量 Ln工资 内生变量 受教育年限 工具变量 母亲受教育年限 成绩 外生变量 婚姻(已婚为1) 是否大城市(1为大城市) 当前单位工作年限 上一表格展示本次研究时涉及的各变量属性,包括被解释变量,内生变量,工具变量和外生变量组成情况。
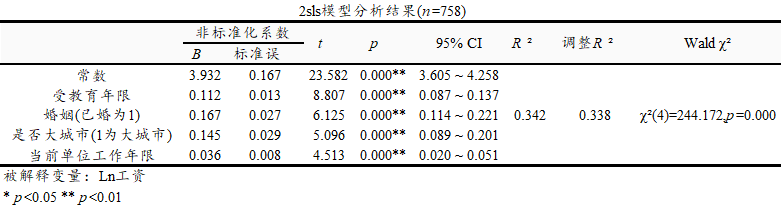
上表格列出TSLS两阶段最小二乘回归的最终结果(第二阶段结果),首先模型通过Wald 卡方检验(Wald χ2 =244.172,p =0.000 <0.05),意味着模型有效。同时R 方值为0.342,意味着内生和外生变量对于工资的解释力度为34.2%。具体查看内生和外生变量对于被解释变量‘工资’的影响情况来看:
受教育年限的回归系数值为0.112(p =0.000<0.01),意味着受教育年限会对工资产生显著的正向影响关系。
婚姻(已婚为1)的回归系数值为0.167(p =0.000 <0.01),意味着相对未婚群体来讲,已婚群体的工资水平明显会更高。
是否大城市(1为大城市)的回归系数值为0.145(p =0.000 <0.01),意味着相对来讲,大城市样本群体,他们的工资水平明显会更高。
当前单位工作年限的回归系数值为0.036(p =0.000 <0.01),意味着当前单位工作年限会对工资产生显著的正向影响关系。
总结分析可知:受教育年限, 婚姻,是否大城市, 当前单位工作年限全部均会对工资产生显著的正向影响关系。
模型汇总(中间过程) Wald χ2 R R 2 调整R 2 Root MSE DW值 χ2(4)=244.172,p =0.000 0.585 0.342 0.338 0.348 1.755 
上表格展示模型的基础指标值,包括模型有效检验wald卡方值(此处提供wald卡方非F 检验),R 值,Root MSE等指标值。
Durbin-Wu-Hausman test外生性检验(test of exogeneity) 检验 原假设 检验结果 检验结论 Durbin检验 所有解释变量均外生(不存在内生变量) χ2(1)=3.973,p =0.046 拒绝原假设 Wu-Hausman检验 所有解释变量均外生(不存在内生变量) F (1,752)=3.962,p =0.047 拒绝原假设 Durbin-Wu-Hausman test用于检验解释变量X(即内生外量)是否均为外生变量(即是否不存在内生变量);从上表格可知,本次研究纳入的内生变量为‘受教育年限’,Wu-Hausman检验显示拒绝原假设(p =0.047 <0.05),意味着‘所有解释变量均外生’这一假设不成立。即意味着‘受教育年限’是内生变量。同时也可使用Durbin检验,一般情况下使用Wu-Hausman检验较多。
-
特别提示
-
如果无法拒绝原假设,那么说明研究的内生变量并不是真正意义上的内生变量,那么此时可考虑直接使用OLS回归结果即可,但多数时候也可直接使用TSLS两阶段最小二乘的结果,似研究者专业理论知识综合而定。
过度识别检验(overidentifying restrictions) 检验 原假设 检验结果 检验结论 Sargan检验 所有工具变量均外生 χ2(1)=0.025,p=0.874 接受原假设 Basmann检验 所有工具变量均外生 Χ2(1)=0.025,p=0.874 接受原假设 过度识别检验用于检验工具变量是否为外生变量,本次研究涉及工具变量为2个,分别是‘母亲受教育年限’和‘成绩’。从上表可知,过度识别Sargan检验显示接受原假设(p =0.874>0.05),同时Basmann检验也显示接受原假设(p =0.874>0.05)。同说明无法拒绝‘工具变量外生性’这一假定,模型良好。
-
特别提示
-
过度识别检验用于判断‘工具变量的外生性’,SPSSAU提供Sargan和Basmann检验,使用其一即可;
-
工具变量个数>内生变量个数,即过度识别时,才会有效;如果恰好识别(工具变量个数=内生变量个数),此时无法输出检验值。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
内生变量和外生变量,其二者均为解释变量,如果考虑内生性问题时才会将解释变量区分成内生变量和外生变量。
-
模型有效性检验上,SPSSAU默认使用wald卡方检验而非F 检验。
-
内生性问题的解决上,除TSLS,通常还可使用GMM估计。
-
-
7、疑难解惑
-
spssau两阶段TSLS时,如何输出第一阶段的预测值和残差值?
-
两阶段TSLS时,默认不会输出第1阶段的预测值和残差值,如果有需要,可用计量研究模型里面的OLS回归,并且选中‘保存预测值和残差’,即可得到第1阶段的预测值和残差值。
-
两阶段回归时输出弱工具变量检验Cragg-Daniels statistic?
-
SPSSAU默认提供第1阶段回归结果,以及第1阶段回归弱工具变量检验Cragg-Daniels statistic,通常情况下其对应的统计量F 值小于10说明可能存在弱工具变量。
-
