泰尔指数分析

泰尔指数是一种衡量‘不平均’的指数，比如用于衡量‘贫富差异’，也或者衡量大气污染的水平是否一致，二氧化碳排放水平差异情况等。泰尔指数的数学原理是‘熵’，‘熵’是一种衡量数据‘有序性’的指标，当‘熵’值越大时，数据越无序，那么意味着‘不平均’情况越严重。

泰尔指数正式分析前需要了解两个基本的名词，如下：

项 说明
泰尔指数类型 T指数、L指数、GE1和GE0
Group项 普通泰尔指数、一阶泰尔指数、二阶泰尔指数

结合具体的泰尔指数计算原理，其可分为四种类型的泰尔指数，分别是T指数、L指数、GE1指数和GE0指数，四种类型的指数在原理上稍有区别，但应用上均是对‘不平均’情况的衡量，其中T指数使用最多。比如研究我国贫富差距‘收入不均’问题，但是每个省的GDP或者人口基数并不一致，即计算泰尔指数的时候，如果某个省GDP更多，或者人口更多，那么其对于整体收不均的影响作用会更高。T指数正是基于GDP作为权重，GDP越大时该省对于整体泰尔指数的影响会越大；类似地，也可使用人口作为权重，当人口越多时，该省对于泰尔指数的影响会越大，L指数正是基于人口作为权重进行计算。基于上述原理，在计算T指数或L指数时，通常需要提供类似GDP和人口共两项数据。

如果提供的原始数在为人均GDP一项（没有GDP和人口两项数据），那么此时则需要使用GE1或GE0指数，其只需要提供人均GDP这样的1项数据进行计算，GE1和GE0是基于广义熵概念计算得到，二者区别在于广义熵时的alpha值，GE1时alpha值为1，GEO时alpha值为0，GE1和GE0指数使用相对较少。

除上述外，还需要理解的一个名词为Group项，计算泰尔指数时，很可能出现‘层次聚集’数据，比如中国包括31省，每个省包括很多个市，每个市包括很多个县，每个县还可包括很多个乡镇。带有此类聚集特征的数据，即具有Group项，比如省份、市、县均为Group项。当数据完全没有Group项时，比如直接31个省（共31行数据）的GDP和人口，计算泰尔指数，此时则称为普通泰尔指数。比如数据包括31个省，每个省比如有6个市，共计31*6=186行数据时（省-》市），此时具有1个Group项即省，此时称为一阶泰尔指数。比如数据包括31个省，每个省比如有6个市，每个市有10个县，那么此处有2个Group项（省-》市-》县），分别是省和市，省的层级最高即Group1，市的层级稍低为Group2，此时计算的泰尔指数称为二阶泰尔指数。

理论上还会有三阶泰尔指数、四阶泰尔指数等，实际情况中由于数据的可获取性及研究目的需要等，实际使用极少，通常情况下一阶泰尔指数较多。SPSSAU默认提供最多两个Group项即最多二阶泰尔指数，如果两个group项均不放入，那么为普通泰尔指数，如果放入1个Group项那么为一阶泰尔指数，如果放入2个Group项则为二阶泰尔指数。

与此同时，在计算泰尔指数时，很多时候需要对比不同年份数据情况，当数据中包括多个年份时，比如最近10年数据，且31个省，每省6个市，共计为10*31*6=1860行时，可将年份进行设置，系统会自动遍历计算出分别10年的泰尔指数。

泰尔指数案例

  • 1、背景

    当前有中国2012 ~ 2021共计10年各省的GDP数据、人口和人均GDP数据，将省分成七大区域（分别是华北、东北、华东、华中、华南、西南、西北），分析中国人均GDP收入的差异情况，对比各大区域的具体差异情况等，部分数据如下图所示：

    明显地，数据中包括1个Group项即‘区域’，并且为10年，共计为310行数据，本案例为一阶泰尔指数，并且为10年分别进行计算对比。如果省份再继续往下细分为市，那么省就是另外一个Group即二阶泰尔指数。

  • 2、理论

    如果计算泰尔指数时，涉及到一阶或者二阶，即当提供的数据具有聚集性时，那么泰尔指数则会进行拆分为比如组内和组间指数。具体说明如下表格:

    项 说明
    普通泰尔指数 只有1个系数值
    一阶泰尔指数 泰尔指数=组内TWR+组间TBR，TWR表示区域内差异情况，TBR表示区域间差异情况
    二阶泰尔指数 泰尔指数=组间TBR+组间TBP +组内TWP ，TBR表示区域间差异，TBP表示省间差异情况，TWP表示省内差异情况

    如果是普通泰尔指数，那么直接就只得到1个泰尔指数值。如果是一阶泰尔指数，比如本案例为‘区域-》省’这样的数结构时，泰尔指数可具体细分为组内TWR和组间TBR，比如本案例分为7个区域，那么7个区域之间的收不均则叫组间TBR，每个区域（比如华北区域）内各个省之间的差异则叫组内TWR。如果是二阶泰尔指数，比如‘区域-》省-》市’这样的数据结构，各个区域之间的差异称为‘组间TBR’，各个省之间的差异称为‘省间TBP’，以及各个省包括很多个市，比如浙江省包括10个市，那么此10个省之间的差异，则称为‘组内TWP’即省内差异情况。

  • 3、操作

    本例子中操作截图如下：

    • 泰尔指数类型选择最常用的T指数，T指数时要求提供GDP和人口共两项数据，以及本案例包括10年，因而将年份放入对应框中。

    • 本案例为一阶泰尔指数（区域-》省）结构，Group项为区域，因而将其放入Group1项中。需要提示的是，案例数据最细粒度单位为省，此处省并不Group项。

  • 4、SPSSAU输出结果

    泰尔指数模型输出泰尔指数分解和贡献值两类结果指标，并且以图形进行展示，说明如下：

    表格/图名称 说明
    泰尔指数分解 一阶或者二阶泰尔指数时则有指数分解
    泰尔指数分解图 以图的形式展示泰尔指数分解结果
    Group项时泰尔指数 展示各Group具体项的泰尔指数值
    Group项时泰尔指数图 图示化展示各Group具体项的泰尔指数值
    Group项时贡献值 展示各Group具体项的贡献值
    Group项时贡献值图 图示化展示各Group具体项的贡献值

    当‘普通泰尔指数’即没有Group项时，仅展示1个泰尔指数值。如果是一阶或者二阶泰尔指数，则会涉及到泰尔指数分解，以及各Group项对应的泰尔指数，以及各Group项时贡献值情况。本案例数据为一阶泰尔指数，因而会输出泰尔指数分解结果，Group项时泰尔指数结果。

    泰尔指数的理解较为简单，但其计算公式相对复杂，为更好地理解泰尔指数原理，下述以一阶泰尔指数的计算公式为便进行说明。

    T=∑i∑j[YijYln⁡(Yij/YNij/N)]Ti=∑j[YijYiln⁡(Yij/YiNij/Ni)]TWR=∑iYiY∑j[YijYiln⁡(Yij/YiNij/Ni)]TBR=∑iYiYln⁡(Yi/YNi/N)

    • 上述四个式子中，T表示整体泰尔系数，Ti表示第i个区域的泰尔系数，TWR表示组内泰尔系数即区域内部泰尔系数，TBR表示组间泰尔系数即区域之间泰尔系数。Ln表示取对数的意思，各个符号说明如下：

    • i: 区域的编号

    • j: 省的编号

    • Y：GDP加总

    • Yi: 某区域gdp

    • Yij：某区域某省gdp

    • N：人口加总

    • Ni: 某区域人口

    • Nij：某区域某省人口

  • 5、文字分析

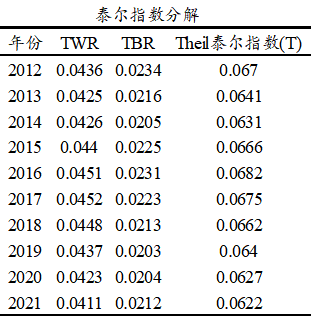
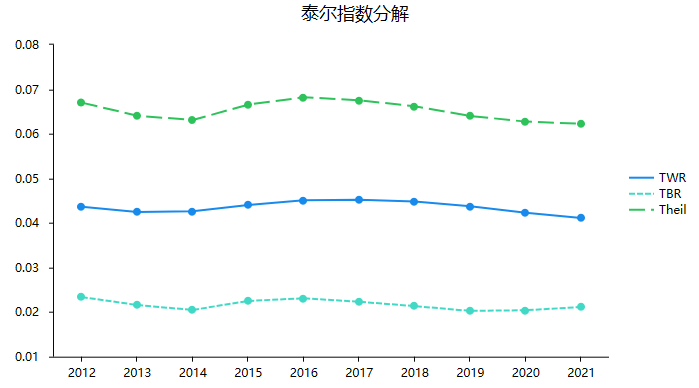
    本案例时泰尔指数分为TWR和TBR，TWR表示组内泰尔系数即各个区域内部的贫富差异（T是泰尔指数的简写，W是within即组内的简写，R是区域Region的简写），TBR表示组间泰尔系数即区域与区域之间的贫富差异情况（T是泰尔指数的简写，B是between即组间的简写，R是区域Region的简写）。整体上看，各个年份上，整体泰尔指数变化不大，意味着各年份对比来看，贫富差异并没有明显的变化，从2016年起泰尔系数稍有减少，意味着贫富差异现象整体上有着微弱的减少趋势。TWR和TBR对比上，TWR相对明显更高，意味着当前的贫富差异主要是体现在区域与区域之间，而区域内部的贫富差异相对较小。泰尔系数分解可见下图。

    • 特别提示：

    • 泰尔指数是基于熵值原理进行计算，泰尔系数的大小并无绝对意义，其只有相对大小意义，并不能说3就比0.1绝对更高，而应该站在同一对比水平上进行对比。

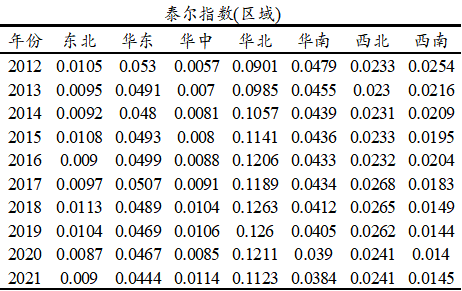
    具体针对各个区域上看，整体对比七大区域的贫富差异情况可知，整体上看，华北地区的贫富差异明显最高，泰尔系数基本均在0.1或者以上，意味着华北地区当前的贫富差异现象相对明显，可能由于北京作为国家行政中心极强，但华北的基它地区，比如河北、山西、内蒙古等省市的收入明显更低导致。接着，华南和华东地区也有着较强的贫富差异现象，但比起华北来看还是较弱。西北地区和西南地区这两个地区贫富差异现象较弱，另外东北地区和华中地区的贫富现象相对最低，意味着该两个地区的人均收水平相对更加均衡。

    除了分析各个区域的泰尔指数得到贫富差异情况外，还可分析各个区域对于整体泰尔指数的影响作用情况即贡献值分析。

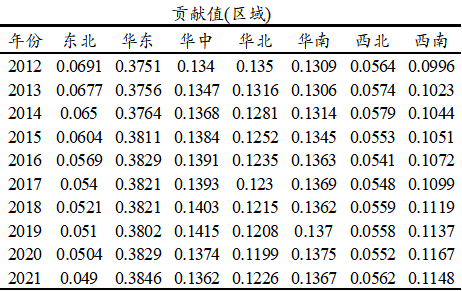
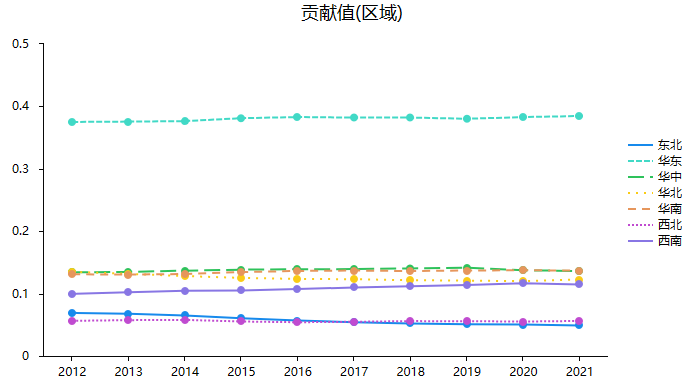
    上表格展示各个区域泰尔指数的贡献情况，本案例数据使用泰尔T指数，其基于GDP作为贡献值大小标准。因而当某区域的GDP越高时其对整体泰尔指数（即整体贫富差异）的作用力度越大。上表格和下图可以看到，整体上看，华东地区的贡献值相对最高，这是由华东地区包括浙江、江苏、山东等经济大省决定。而华中、华北、华南对于整体贫富差异的影响作用力度较高，西南地区次之，东北和西北这两个地区对于泰尔指数的作用力度相对最小。

  • 6、剖析

    • 泰尔指数分析涉及以下几个关键点，分别如下：

    • 特别注意正确的数据格式。比如是‘省-》市’数据，即最小粒度单位是市，那么有两列分别标识省和市，但省才是聚集性group。如果有多年数据，那么其仅仅是重复，行数成年份倍数增长而已。

    • 泰尔指数包括四种类型，T指数、L指数、GE1和GE0，T指数和L指数时，需要传入比如GDP和人口这两项数据，因为衡量不平均是由人均GDP决定，T指数计算贡献值时使用GDP这样的数据，L指数计算贡献值时使用人口这样的数据，其中T指数使用最多。GE1和GE0这两个指数使用相对较少，其利用广义熵进行计算，而且其要求传入的数据为比如人均GDP这1个数据，GE1时贡献值是由group内样本个数及数据大小共同决定，GE0时贡献值是由group内样本个数决定。