季节性Sarima模型,其是在arima模型(移动平均自回归模型)基础上多出一个季节性(seasonal)。比如某旅游景点的销售额数据,每年中有夏天的6/7/8共3月为旺季,但是其它时间是淡季,但每年整体的销售额均呈现出一定逐步上升趋势。在模型构建时就需要考虑该周期性因素,即此处的周期值S=12(1年为12月)。Sarima模型正是处理此类带有明显周期性的时间序列数据而生,其它理论内容与arima基本一致。除开上述中的参数值即周期值S=12,Sarima模型还涉及另外3个参数值即P/D/Q,此这3个参数值与arima模型的p/d/q意义保持一致。具体细节内容可参见SPSSAU中arima帮助手册。
对于Sarima模型的构建时,建议有三种方法。1是SPSSAU自动化法,即设置好周期S值后,另外p/d/q/P/D/Q共6个参数值由系统自动寻优找到;2是半自动法,研究者可试图先找出一些可能的参数值模型,然后记录下该模型的AIC/BIC/均方根误差RMSE指标,并且针对多个模型进行对比,AIC/BIC这两个信息准则值越小意味着模型越优,类似地均方根误差RMSE指标表示模型残差的平均gap值,该指标也是越小越好,对比多个潜在模型然后先出最优模型;3是纯手工建模法,即分别找到差分参数值d/D值,以及结合偏自相关图主动判断得到p/q/P/Q四个参数值,相对来看,纯手工建模法较为复杂且带有较强的主观性,并且在Sarima模型时有时候数据量较小导致无法有效的观察得到P/Q参数值等,因而建议研究者直接使用自动化法,也或者半自动法建模。
关于手工建模法,其有着一定的主观性且其并没有固定的分析流程,SPSSAU建议研究者可按下述步骤进行模型构建,分别如下:
| Step | 说明 |
|---|---|
| Step 1 | 结合图和专业知识,得到周期值S |
| Step 2 | 进行‘周期差分’,即D=1或者0 |
| Step 3 | 判断是否平稳,如果平稳则d=0,不平稳做差分直至平稳,此时差分阶数值即为d值 |
| Step 4 | 基于第3步后的数据,结合ACF/PACF图,判断p和q值 |
| Step 5 | 基于第3步后的数据,结合ACF/PACF图,判断P和Q值,查看阶数的时候需要查看‘滞后阶数/S’(比如S=12,那么滞后阶数12其实是季节性的滞后1阶) |
首先需要知道S值即季节性周期值,正常情况下专业角度可以确定好,如果无法确定建议使用‘时序图’直观查看和判断周期值。接着进行周期差分即得到D值,正常情况下D值为1或者0即可(0是指不做季节性差分),如果D值过大会导致模型过于复杂且准确性下降(经验法则得到)。接着基于第2步后,得到新的数据(可使用SPSSAU生成变量功能进行季节性差分)进行平稳性判断和分析(时序图或者单位根检验),继而得到d值。接着基于3步之后数据,进行判断p/q/P/Q值,需要注意的是p值和q值需要在一个周期S范围内观察,而P/Q值的判断和观察应该基于第i时刻,第i+S时刻,第i+2S,第i+3S依次下去时刻的滞后阶数去判断P/Q值。以及多数情况下P/Q值应该尽量小,原因在于时间序列数据通常较少且P/Q值过大时,其对当前数据的预测作用减弱。在得到各个参数值后,主动设置参数值进行分析,得到预测结果等。
季节Sarima案例
-
1、背景
当前有2016.1 ~ 2022.11共计83个月度的新能源汽车销售数据,数据来源于乘联会官网报告整理。众所周期,从2015年起新能源汽车销售具有逐年增长趋势,并且每年均有季节性周期波动,比如年前通常是高峰期,但年后是低谷期。直观上看,当前数据非常适合进行Sarima模型构建,部分数据如下:
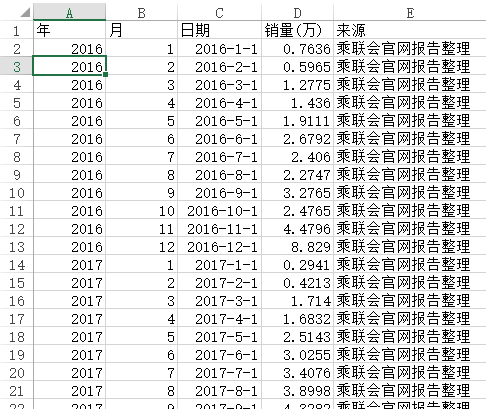
-
特别提示:
-
时间序列的数据格式上,一定是时间从上至下递增,而且不能有间隔,比如2015,2017,2018这种数据少了2016,这类数据不能称为时间序列数据。
-
时间序列的单位一般是年,比如我国历年的GDP数据,也或者我国历年人口数据等。当然如果单位是月或者季度,也或者周等,可以体现出数据的变化规律,也一样可以作为时间序列数据使用。本案例数据单位是月。
-
-
2、理论
本次Sarima模型构建时,直接使用SPSSAU系统自动寻优方式进行,有兴趣的研究人员可进行比如手工建模法等。
-
3、操作
本次研究希望SPSSAU自动拟合出最佳的ARIMA模型,因此不设置p/d/q/P/D/Q共6个参数值,但S值需要进行设置,当前设置为12。操作如下图:
-
4、SPSSAU输出结果
SPSSAU共输出5个表格和1个图形,如下所示:
项 说明 SARIMA模型参数结果 展示p/d/q/P/D/Q等参数值 SARIMA模型参数表 展示模型具体拟合参数值,意义较小,但其中的AIC和BIC值意义较大 预测值 展示模型预测值,并且展示均方根误差RMSE值 预测值图形展示 图形化展示模型拟合和预测情况 模型残差检验结果 针对当前模型进行残差检验,判断模型质量效果等 模型Q统计量表格 展示残差Q检验结果,检验模型残差白噪声情况 -
5、文字分析

上表格显示p/d/q/P/D/Q参数信息值,从上表格可以看到,本次模型为Sarima(0,1,1)(0,1,3),S值为12。d/D这两个差分值均为1。
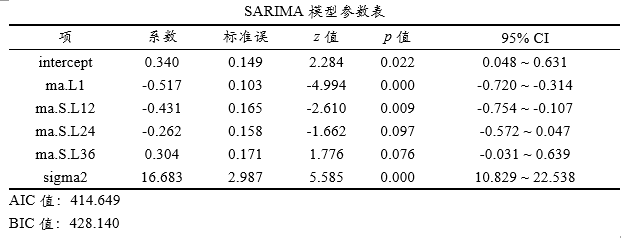
上表格展示模型构建结果,包括模型参数和信息准则。本次模型构建时,SPSSAU自动构建出模型为:Sarima(0,1,1)(0,1,3),上表格中ma表示移动平均的意思,L1表示滞后1阶的意思,L12表示滞后12阶的意思,由于Q=3,因而会出现L12/L24和L36。如果研究人员希望自己进行模型构建并且进行优劣对比,可先记录下每个模型的AIC或BIC值,然后结合AIC或BIC值越小越好的原则,选择最优模型。

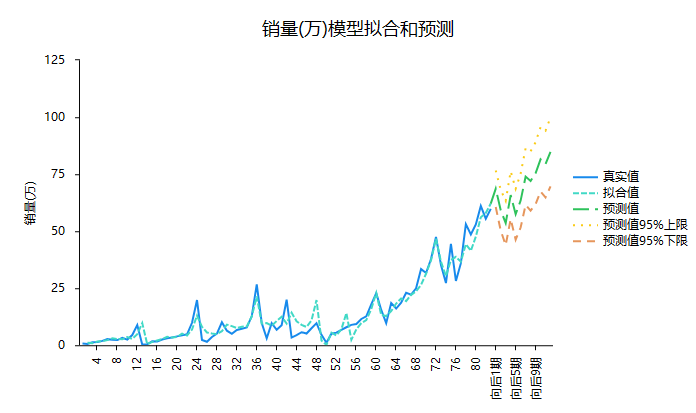
上表格展示预测值,其最为重要。向后1期即指2022年12月(数据最后一期是2022.11月),向后2期是指2023.1月数据。通常情况下向后一个周期内的数据相对较为准确,向后期数越多可能准确率越低。本次预测2022.12月新能源汽车销售量为68.653万,2023.1月销售为59.205万。
SPSSAU默认展示时间序列最近12期的实际值和拟合值和预测数据。可通过下图直观查看数据拟合效果等。
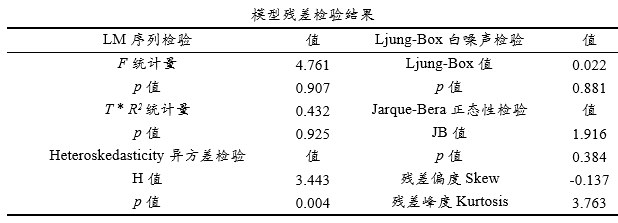
上表格展示出sarima模型各类残差检验指标;包括拉格朗日乘数检验(Breush-Godfrey LM检验),其用于检验模型残差序列是否存在序列相关,其原假设H0为序列不存在序列相关,备选假设H1为序列存在序列相关, LM检验提供两个统计量分别是F和T * R方,通常使用F统计量即可;
Ljung-Box白噪声检验用于检验模型残差是否满足白噪声,其原假设H0为序列为白噪声,备选假设H1为序列非白噪声;Heteroskedasticity异方差检验用于检验模型残差是否存在异方差,其原假设H0为序列不存在异方差,备选假设H1为序列存在异方差;Jarque-Bera正态性检验用于检验模型残差是否满足正态性,其原假设H0为序列满足正态性,备选假设H1为序列非正态性;
通常情况下希望序列均接受原假设H0即残差序列不存在序列相关、满足白噪声、不存在异方差问题并且满足正态性。但实质研究中,很难各项均满足,比如本案例数据,满足LM检验即序列相关,Ljung-Box白噪声检验,而且满足Jarque-Bera正态性检验。但并不满足Heteroskedasticity异方差检验。一般来说满足白噪声检验更加重要,本案例数据模型满足此检验,除此之外,SPSSAU还单独提供Q检验,与Ljung-Box检验类似,其也用于白噪声检验。
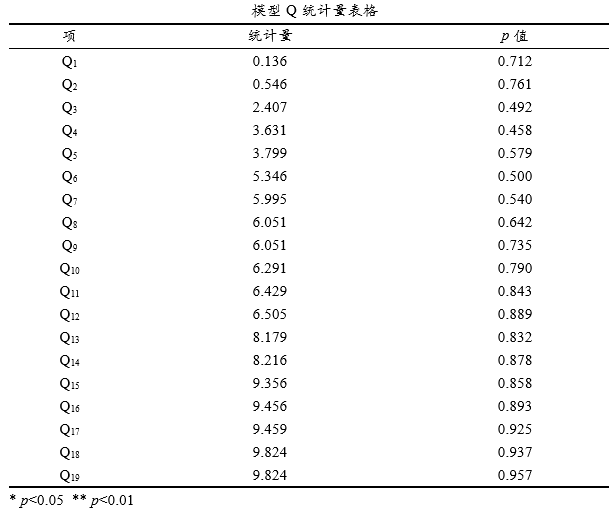
Sarima构建后一般要求模型残差为白噪声,可通过Q统计量检验进行白噪声检验(原假设:残差是白噪声);比如Q6用于检验残差前6阶自相关系数是否满足白噪声,通常其对应p 值大于0.1则说明满足白噪声检验(反之则说明不是白噪声),常见情况下可直接针对Q6进行分析即可;从Q统计量结果看,Q6的p 值为0.5大于0.1,则在0.1的显著性水平下不能拒绝原假设,模型的残差是白噪声,模型基本满足要求。
-
6、剖析
-
涉及以下几个关键点,分别如下:
-
SPSSAU默认自动寻优找出最佳参数并且进行预测,研究人员也可多次自行构建模型,并且对比模型拟合优劣指标比如AIC/BIC和RMSE值等,然后对比选择较优模型。
-
模型残差性的判断上,有很多测量维度,包括白噪声检验,正态性,自相关性,异方差性等,通常很难都满足,但一般希望通过白噪声检验。
-
疑难解惑
-
SPSSAU中Sarima模型保存拟合值?
-
SPSSAU进行Sarima模型时,可选中开始分析按钮右侧‘保存残差和预测值’参数,系统会自动新生成两个标题来标识对应的预测值和残差。
-
SPSSAU进行arima预测时的RMSEA指标意义?
-
RMSEA的意义为残差平方和的平均值并且开根号,即平均的残差值情况,SPSSAU默认输出该指标值。
-
RMSE、MSE、MAE和MAPE这4个指标分别什么意义?
-
RMSE(均方根误差),其表示模型拟合后的平均残差情况如何,即模型拟合后真实值与预测值之间的偏差有多大,该值越小越好;
-
MSE(均方误差),其表示模型拟合后的平均残差平方值如何,MSE开根号即为RMSE值,该值越小越好;
-
MAE(平均绝对误差),其为残差的绝对值之和,然后求平均值,其表示平均偏差是多大,与RMSE的意义基本一致,该值越小越好;
-
MAPE(平均绝对百分比误差),其为残差除以真实值的绝对值之和,然后求其平均。该值为相对指标值,其表示预测值与真实值之间gap平均偏离真实值的比例情况,比如为0.2,其表示平均偏离真实值20%左右,该值越小越好,并且该指标值具有比较意义,不同模型之间均可对比该值的相对大小,进而衡量模型优劣情况。