断点回归是一种‘准自然实验’式研究,其思想在于存在一个连续变量(驱动变量X,或分组变量,或处理变量),该变量某临界点cutoff处可拆分成左侧和右侧,进而研究该变量对于另一变量(结果变量Y,或因变量)的影响。比如高考时本科线为500分,那么有的学生好低于500分,有的弱高于500,但正是由于500这个cutoff断点值,导致学生是否能上本科,进而最终影响到学生以后的收入情况,此处高考成绩即为驱动变量X,收入则为结果变量Y。
上述的500分是一个非常明确的断点cutoff值,如果低于500分一定不能上本科,高于500分一定可以上本科,那么此类RDD模型则称为‘精确断点’(sharp regression discontinuity design, 简称SRD)。如果说有的学生有着‘特长加分项’,分数小于500分但正由于其有着‘特长加分项’因而上了本科,也或者有的学生高于500分但是其更愿意读了优秀的专科,此类情况时的断点回归研究,称作为‘模糊断点回归’(fuzzy regression discontinuity, 简称FRD),多数情况下研究均使用精确断点SRD;除此之外,RDD断点回归模型时有时还会加入到控制变量。上述涉及几个关键术语,汇总如下表:
| 名称 | 说明 |
|---|---|
| 结果变量Y | 也称因变量 |
| 处理变量或驱动变量X | 也称自变量 |
| 断点值 | 可将处理变量X明确拆分成两组的cutoff值 |
| 控制变量 | 可能对模型产生干扰的项 |
| Fuzzy模糊项 | Fuzzy项 |
RDD断点回归案例
-
1、背景
一般来讲美国民主党更倾向于更多的联邦支出,案例研究是否民主党获选对于联邦支出的影响。通常情况下如果得票率大于50%即会获选,反之小于50%则会落选。因而得票率则为驱动变量X,此处0.5则可作为断点cutoff值(研究中为了方便使用,因而将得票率 – 0.5)作为驱动变量,即最终cutoff值为0,大于0则应该获选,小于0则应该落选)。结果变量Y为联邦支出。而且还包括另外2个控制变量。除此之外,还包括另外一个变量‘是否获选’作为判断是否模糊断点。本案例数据使用Stata软件的votex.sta数据,各数据的定义如下:
项 变量简称 变量说明 结果变量Y y Log fed expenditure in district 处理变量或驱动变量X x Dem vote share minus .5 模糊变量fuzzy项 fuzzy Dem Won Race 控制变量 control1 Incumbent 控制变量 control2 Voting Age Population Share -
2、理论
RDD断点回归的分析知识点相对较多,从分析步骤包括,具体可精确断点或模糊断点的选择,模型选择,模型基本假定分析,模型分析,模型稳健性检验等。具体分为以下5步。
第一步、精确断点和模糊断点判断判断精确断点或模糊断点的思路在于处理变量X被cutoff分为左右两侧后,是否真正决定‘实验走向’,比如本案例中cutoff值分成两组后即认为‘民主党是否当选’(命名为new_x),而fuzzy模糊项即真实是否当选项,如果与new_x与fuzzy项没有特别明显的不一致,甚至完全一样,此时则应该使用精确断点。反之如果new_x与fuzzy项有着明显的差异,此时使用模糊断点较为适合。
第二步、模型选择,通常指模型阶数的判断研究X对于Y的影响时,二者的关系是线性关系(一阶),还是曲线二阶关系,也或者三阶关系。可首先通过图示直观查看,并且得出结论。待定模型阶数后,后续分析基于该阶数进行分析使用。至于‘带宽值’或者‘核函数’,通常默认即可,SPSSAU会自动找出最优带宽值,默认使用triangular三角核函数。
第三步、模型基本假定分析RDD模型通常包括着一定的假设,通常包括‘断点适用性检验’和‘局部平滑性检验’。如下所述:
第四步、模型分析假定 说明 SPSSAU是否提供 断点适用性检验 驱动变量不应存在人为操控,正常情况下断点cutoff值附近样本量基本一致才会具有随机性 通过图示直接查看断点左右两侧样本量密集性情况,如果出现一侧明显更多样本点则说明不适合 局部平滑性检验 如果有控制变量,那么控制变量在断点处不应该存在明显的跳跃现象 将控制变量看成‘驱动变量X’进行分析,图示查看即可 在上述确认好精确或模糊断点,并且确定好模型阶数,并且模型适合时,则开始分析X对于Y的影响关系情况。
第五步、模型稳健性检验模型分析后,还需要对模型稳健性进行检验。模型稳健性检验有多种方式,包括更换核函数法、更换断点值法,是否加入控制变量法,更换带宽值法,更换阶数,改变样本选择法,如下表格所述。
稳健性检验方式 说明 SPSSAU是否提供 更换核函数 更换不同核函数时结论是否稳定 研究者更换核函数 更换断点 更改不同断点值时,结论是否稳定 研究者更换断点 是否加入控制变量 是否加入控制变量时,结论是否稳定(断点安慰剂检验Placebo Tests) 研究者更换模型,即是否加入控制变量 换带宽 更换带宽值时,结论是否稳定 自动提供,且提供coefplot图 换阶数 更换阶数时,结论是否稳定 研究者更换阶数 样本选择 更换筛选样本时,结论是否稳定 研究者自行处理 -
3、操作
第一步、精确断点和模糊断点判断将X按cutoff值0分为两组,并且与fuzzy项进行交叉卡方分析。操作截图分别如下:
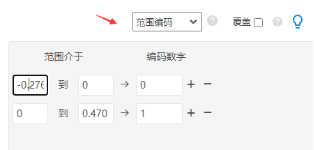
使用SPSSAU数据处理->数据编码功能,并且选择‘范围编码’,将x按cutoff值0分为两组(可通过描述分析得到x的最小值为-0.276,最大值0.470)。系统会自动生成一个新标题‘New_x’,将该项与fuzzy项进行交叉卡方,得到如下结果:
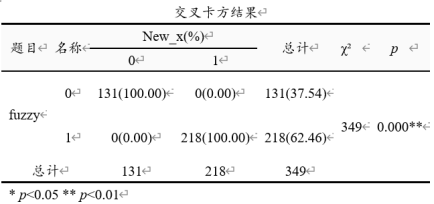
New_x代表x分为两组后的新变量,0代表cutoff值左侧(落选),1代表cutoff值右侧(当选)。而fuzzy项里面的0和1代表真实情况下‘是否当选’(0为落选,1为当选)。从上表格可以看到:二者数据完全一致,按cutoff值得到的131个‘落选’样本真实情况下也是‘落选’,按cutoff值得到的218个‘当选’样本真实情况下也是‘当选’。即意味着应该使用精确断点。
-
提示:
-
实际研究中,如果数据的gap较小,此时也可直接使用精确断点回归。
确认好为精确断点模型之后,接着进行第二步。
第二步、模型阶数判断模型阶数判断时使用直观图示法。即首先进行模型分析,通过图示查看模型应该是一阶、二阶或三阶更加适合。首先操作如下图:
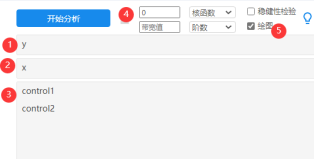
首先放入结果变量y,驱动变量x,2个控制变量。以及设置好断点值为0(默认不设置即结果变量的中位数),选中‘绘图’复选框。至于另外4个参数(带宽值、核函数、阶数和稳健性检验)默认即可。此步骤主要查看绘图,用于确认‘阶数’。得到图形如下:
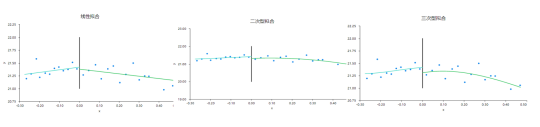
从上图可以看到,最左侧‘线性拟合’即一阶时或者中间‘二次型拟合’即二阶时,模型拟合相对较好。可能‘二次型拟合’相对更适合。因而确定模型为二阶。并且后续以二阶为准进行分析。另外从上面三个图可以看到,断点值左右两侧附近的样本量基本均匀,即说明断点值选择适合没有受到人为操纵。
第三步、模型基本假定分析模型基本假定分析时,通常包括‘断点适用性检验’和‘局部平滑性检验’。关于‘断点适用性检验’如果说cutoff值两侧附近的断点样本量基本均匀则说明断点选择适合,不受人为操纵。从第二步中得到的图形也可以看出,断点值附近两侧的点基本差不多,说明当前案例设置的断点值准确,并没有受到人为操纵干扰。
除此之外,还需要查看‘局部平滑性检验’,即分别将控制变量作为驱动变量X进行断点回归,通过图示法查看断点值是否在控制变量身上也起效果,即‘同样的断点值不应该在控制变量身上也起作用’,此检验通常并不完全需要。并且有时候控制变量并不能被当前断点cutoff值区分为两侧因而不能进行分析,本案例即是此类情况,本案例不进行‘局部平滑性检验’。
第四步、模型分析第一步确认好模型为精确断点,并且第二步确定为二阶模型最优,而且满足基本模型假定。因而进行操作,准备得到最终结果。操作如下图所示:
分别设置结果变量y,驱动变量x,2个控制变量。以及设置好断点值为0(默认不设置即结果变量的中位数),设置为‘二阶’,选中‘稳健性检验’复选框。至于另外2个参数(带宽值、核函数)默认即可,并且将‘绘图’复选框取消(因为已经不再需要通过图示查看阶数)。此步骤为了得到最终结果。见‘SPSSAU输出结果’部分说明。
第五步、模型稳健性检验在得到模型最终结果时,选中‘稳健性检验’复选框,系统默认提供不同带宽值(0.25倍、0.5倍、0.75倍、1倍、1.25倍、1.5倍、1.75倍和2倍共8个不同带宽值)时的结果,便于进行稳健性检验查看,实际研究中,可能并不需要8个不同带宽值情况下的结果对比,通常只需要1倍带宽值附近(比如0.75倍、1倍和1.25倍)共3项带宽值时结果对比,如果结论基本稳定即说明模型具有稳健性。
模型稳健性检验并没有固定的做法,只要可以证明模型具有稳健性(不同情况下模型结论基本一致则说明具有稳健性),具体稳健性方式上有很多种,一般使用1种或2种即可并没有固定标准。
至于其它的方式,比如‘更换核函数’法,‘更换断点’法,‘是否加入控制变量’法,‘更换阶数’法和‘样本选择法’。研究者可自行更换模型进行结果对比研究。尤其是‘更换核函数’法,‘是否加入控制变量’法和‘更换阶数’这3种方式,其操作简单方便,只需要在SPSSAU系统中下拉选择下参数更换即可进行,建议研究者尝试使用查看对比即可。比如‘更换核函数法’,操作截图如下所示:
SPSSAU默认是使用‘triangular三角核函数’,可选为‘Epanechnikov核函数’和‘Uniform核函数’,来回切换另外两个核函数,将结果进行汇总对比即可,如果结论基本一致则说明模型具有稳健性。
-
-
4、SPSSAU输出结果
针对本案例结果,即‘精确断点’且‘二阶模型’时结果,SPSSAU共输出表格和图形,具体说明如下:
名称 说明 RDD基本情况 展示结果变量、处理变量、控制变量或fuzzy项对应的项名称 RDD参数情况 展示模型的参数值情况,包括断点值,带宽值,核函数,阶数和是否进行稳健性检验 RDD样本数据情况 展示RDD断点模型,断点值及断点两侧的样本量情况 RDD断点回归结果汇总 展示模型最终结果 稳健性检验-不同带宽时 展示不同带宽值时,模型汇总结果 稳健性检验(基于不同带宽) 不同带宽值时模型回归系数95%置信区间coefplot图 -
5、文字分析
本案例得到最终结果,包括RDD基本情况、RDD参数情况、RDD样本数据情况、RDD断点回归结果汇总,稳健性检验结果和稳健性检验coefplot图,分别说明如下:
RDD基本情况
项 名称 结果变量 y 处理变量或驱动变量 x 控制变量 control1 control2 Fuzzy模糊项 - 从上表格可以看到结果变量、处理变量、控制变量或fuzzy项对应的项名称,本案例中有两个控制变量,另本案例最终为精确断点,因而没有设置fuzzy模糊项。
RDD参数情况
参数 名称 断点值 0 带宽值 0.096 核函数 triangular 阶数 2阶 稳健性检验 是 从上表可以看到,断点值为0,并且没有设置过带宽值,模型自动计算出‘最优带宽值’为0.096,并且默认使用三角triangular核函数,模型设定为2阶。以及选中‘稳健性检验’,SPSSAU自动会提供不同带宽值时模型汇总结果。
RDD样本数据情况
项 数据 断点值 0 断点值左侧样本量 131 断点值右侧样本量 218 分析样本量 349 上表格可以看到,断点值为0,断点值左侧样本量为131个,右侧为218个,总共分析样本量为349个。
RDD断点回归结果汇总
Method Coef. Std. Err. z 值 p 值 95% CI Conventional -0.432 0.257 -1.678 0.093 -0.937 ~ 0.073 Bias-Corrected -0.494 0.257 -1.917 0.055 -0.998 ~ 0.011 Robust -0.494 0.288 -1.716 0.086 -1.057 ~ 0.070 上表格可模型结果核心表格,从上表格可以看到,p 值均大于0.05,但是小于0.1,也即意味意味着如果以0.1作为显著性水平,那么回归系数呈现出显著性,如果以0.05作为标准,则说明没有显著性。无论是Conventional法,也或者校正bias法(Bias-Corrected),也或者稳健法检验robust时。
-
提示:
-
断点回归时对于回归系数的检验共提供3种方式,分别是Conventional法、Bias- Corrected和Robust法,三种方式并没有优劣之分。通常使用其中一种即可,比如Conventional法。下述基于不同带宽稳健性检验时默认汇总Conventional法。
稳健性检验-不同带宽时
带宽值 Coef. Std. Err. z 值 p 值 95% CI 0.024(0.25倍) -0.255 0.533 -0.478 0.633 -1.299 ~ 0.789 0.048(0.5倍) -0.69 0.398 -1.732 0.083 -1.471 ~ 0.091 0.072(0.75倍) -0.544 0.312 -1.742 0.081 -1.156 ~ 0.068 0.096(1倍) -0.432 0.257 -1.678 0.093 -0.937 ~ 0.073 0.119(1.25倍) -0.439 0.235 -1.864 0.062 -0.900 ~ 0.023 0.143(1.5倍) -0.35 0.22 -1.59 0.112 -0.781 ~ 0.081 0.167(1.75倍) -0.218 0.202 -1.081 0.28 -0.613 ~ 0.177 0.191(2倍) -0.143 0.19 -0.751 0.452 -0.515 ~ 0.230 由于本案例时选择‘稳健性’检验,因而SPSSAU提供上表格展示不同带宽值(0.25倍、0.5倍、0.75倍、1倍、1.25倍、1.5倍、1.75倍和2倍共8个不同带宽值)时回归系数显著性检验结果,默认汇总Conventional法的显著性检验结果。从上表格可以看到,8种情况下时,只有其中4种带宽下呈现出0.1水平显著性,另外远离1倍较远的带宽时并没有呈现出显著性。
整体上看,如果模型以0.1作为显著性水平,那么模型具有一定的稳健性(如果是0.05作为标准,则稳健性非常强,因为全部p值均大于0.05)。建议还可进一步通过其它方式,比如‘更换核函数’法,‘是否加入控制变量’法和‘更换阶数’等进一步查看。本案例中如果使用‘更换核函数’,‘是否加入控制变量’或者‘更换阶数’,也会有出现0.1水平显著的结论(但并不完全是),但全部均会出现0.05水平不显著的结论,即意味着如果模型以0.1作为显著性标准,此时模型稳健性较弱,而模型以0.05水平作为标准,此时模型稳健性非常强,无论如何显著性值均大于0.05,最终模型以0.05作为显著性水平,即意味着模型并不显著,即‘民主党当选对于联邦支出并没有实际性影响’,并且此结论非常稳健。
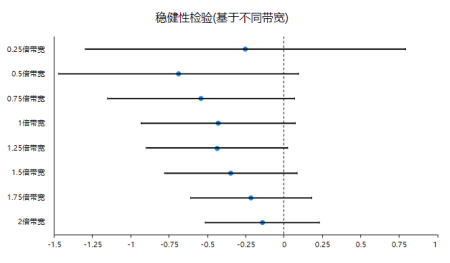
上图为基于不同带宽时,模型回归系数95%置信区间进行展示的coefplot图,从图中可以看到,8种不同带宽时,95%置信区间均包括数字0,即明显的可以看到,模型在0.05水平上不显著,此结论稳定。
-
-
6、剖析
-
涉及以下几个关键点,分别如下:
-
RDD断点回归时,分析步骤较多,建议逐步进行,且在判断时尽量多的对比综合分析,而不能只查看某一个模型基础上得到最终结论;
-
多数情况下使用精确断点,如果确实有非常强的理由证明应该使用模糊断点,也可使用模糊断点;
-
模型阶数判断上结合图示进行,但带有一定的主观性,建议对比选择;
-
模型假定分析时,图示直观上满足即可,不太可能模型完美的满足;
-
模型分析时有3种显著性检验方式,选择其中一种即可;
-
模型稳健性检验有很多种方式,通常选中一个或者两个即可。
-
如果不设置断点值,默认系统会以结果变量的中位数作为断点值。
-
疑难解惑
-
断点回归总是提示‘数据质量异常’?
-
断点回归对于数据的要求较高,如果设置多个断点值后依旧提示质量异常。建议对X即驱动变量进行检验,一般情况下X驱动变量需要为连续数据,如果不是则较容易出现无法计算即数据质量问题。
-
RDD断点回归时总是出数据质量异常?
-
RDD断点回归是一种准自然式实验,其对分析数据使用及数据格式有着严格要求,建议确认。其研究X对于Y的影响时,X可按某断点分成两组,X通常是连续数据。比如研究高考成绩对于收入的影响,X是高考成绩,Y是收入,X可按本科录取最低分值(比如500分)分成两组,低于500分为没能上本科,大于等于500分为可以上本科。那么RDD实际上是研究‘是否上本科’对于收入的影响,但‘是否上本科’这个数据是通过高考成绩(并且加上断点值即本科录取最低分值)进行分拆从而体现‘是否上本科’这一变量的。RDD时无法直接体现‘是否上本科’这一变量,因而使用高考成绩进行替换,这即是RDD的精髓即 ‘准自然式实验’。与此同时,RDD断点回归与双重差分DID思想上有一些类似,请确保使用正确的方法。
-
SPSSAU进行分析时提示‘超时’或‘请求超时’?
-
在某些分析时,比如malquist/dea/rdd断点回归/零膨胀负二项回归等时,其计算量可能较大导致系统无法在非常快的时间内计算出结果,因而会提示‘超时’。此种情况下建议稍等5分钟,然后刷新页面,即可看见‘分析结果列表’中出现新的分析结果,点击打开即可。如果5分钟后还是没有结果,最简单的处理是在EXCEL中对数据进行删减(比如5万行数据变成2万行)后重新上传分析,以及也可以页面右上角反馈人工客服辅助查看处理(提问时,需要提供数据和操作截图共两项)。
