Moran指数(莫兰指数)是研究空间关系的一种相关系数值,比如研究中国31省市GDP之间是否具有空间相关关系。Moran指数通常分为两种,分别是全局Moran指数和local局部Moran指数。全局Moran指数用于分析整体上是否存在空间相关关系,如果全局Moran指数呈现出显著性,接着可进一步深入分析局部Moran指数了解细节性关系情况等。
Moran指数的计算上需要提供两项数据,分别是分析项数据,比如中国2021年GDP数据。除此之外,还需要提供‘空间权重矩阵’数据,‘空间权重矩阵’数据用于标识中国31省市之间的‘邻接’关系情况。‘空间权重矩阵’通常分为两类,分别是‘邻接矩阵’和‘距离权重矩阵’。‘邻接矩阵’使用0和1来标识省份之间是否有‘接壤’关系,0代表没有‘接壤’关系,1代表有‘接壤’关系。‘距离权重矩阵’使用具体数字表示省份之间的距离情况,此处的距离可为实际空间距离,也可以是经济距离等。通常情况下,使用‘邻接矩阵’较多。
更多关于‘空间权重矩阵’的内容,建议研究者查阅相关资料,包括‘邻接矩阵’的构造原理上,比如使用车相邻(Rook)、象相邻(Bishop)或后相邻(Queen)法等构造邻接矩阵等。SPSSAU系统进行Moran指数时,需要传入‘空间权重矩阵’和‘研究项’共两项数据即可进行计算。
Moran指数案例
-
1、背景
当前有2021年中国31省市的GDP数据,并且有计算好的‘邻接矩阵’数据,现希望研究2021年中国31省市GDP是否存在着空间相关关系,以及希望深入挖掘出一些潜在价值信息。当前的部分数据截图如下:
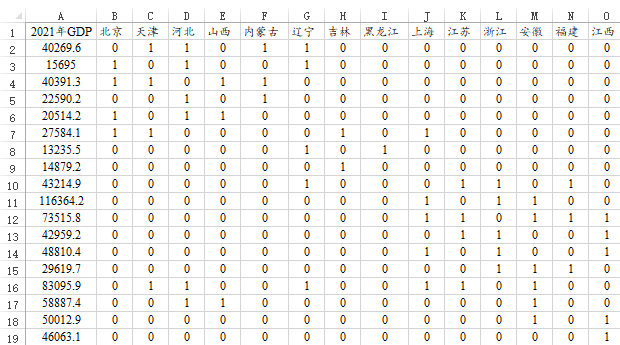
数据中包括2021年31省市的GDP数据,并且包括31省市的邻接权重矩阵,在分析时,首先上传数据,并且在分析时下拉选择‘2021年GDP’项,而邻接权重矩阵通过粘贴方式放入即可。
-
2、理论
Moran指数研究空间相关关系,首先分析全局Moran指数是否呈现出显著性,如果是则意味着存在着空间相关关系,接着可深入分析局部Moran指数,并且结合Moran散点图及研究对象所在象限分布情况,进一步挖掘潜在价值结论。
-
3、操作
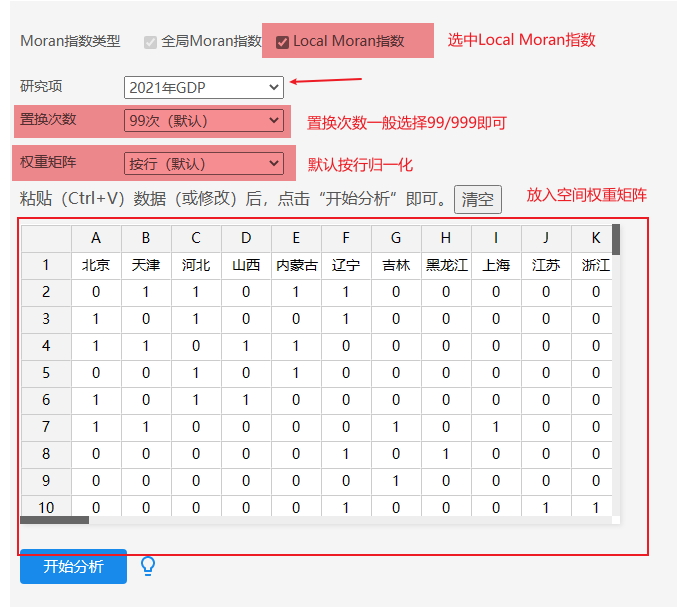
本例子中操作截图如下:
-
选中‘Local Moran指数’,则会计算局部Moran指数值;
-
下拉选择本案例研究项,即2021年GDP;
-
置换次数:莫兰指数检验即p 值计算是通过蒙特卡罗原理计算,一般置换次数越大检验稳定性越强,但该值越大计算量越大,常见选择99次或者999次即可;
-
权重矩阵:该参数代表‘空间权重矩阵’的标准化方式,默认是按行,可选按列标准化处理,通常情况下默认按行即可。
-
空间权重矩阵:EXCEL粘贴框中放入空间权重权重,并且第1行标识研究对象名称,空间权重矩阵为n*n数据结构。
-
-
4、SPSSAU输出结果
moran指数模型一共输出3个表格和1个图,说明如下:
表格/图名称 说明 全局Moran指数 展示全局Moran指数及其检验 Local Moran指数 展示Local Moran值及其检验等 Moran散点图 输出Moran散点图 象限分布表格 输出Moran散点图中研究对象在的象限位置 -
5、文字分析
全局Moran指数 研究项 Moran指数I 期望E(I) 标准差sd(I) z 值 p 值 2021年GDP 0.214 -0.033 0.108 2.137 0.016 从上表可知:全局Moran指数为0.213,并且呈现出0.05水平的显著性(z =2.137, p =0.016),意味着中国31省市2021年GDP具有空间相关关系,而且是空间正相关关系,即具有一定的空间正向聚集关系。接着具体分析局部Moran指数,找到更深入的分析信息。
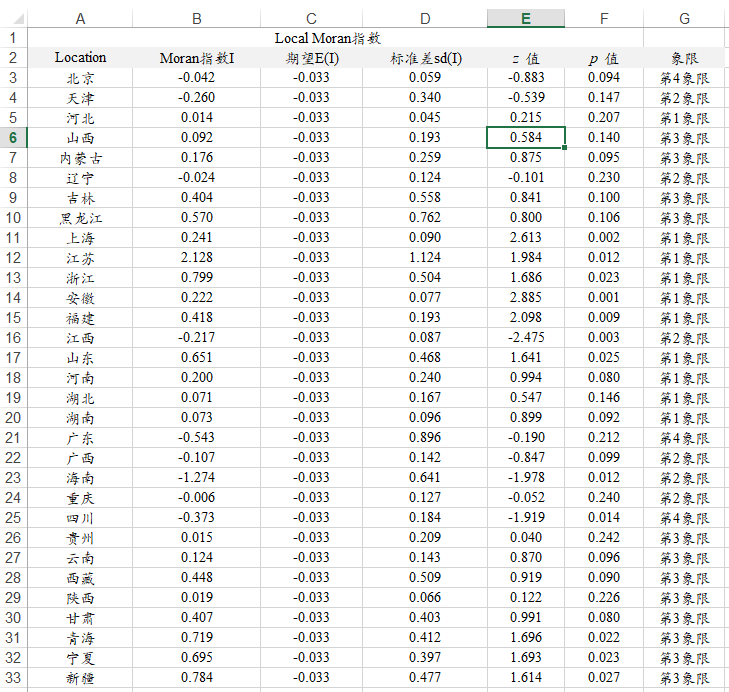
上表格展示局部Moran指数信息及其检查值,而且将31省市在Moran散点图中的象限位置也放在整理在一个表格中便于分析使用。由于数据信息量过大,因而在EXCEL中先筛选出显著性的省份数据如下图:
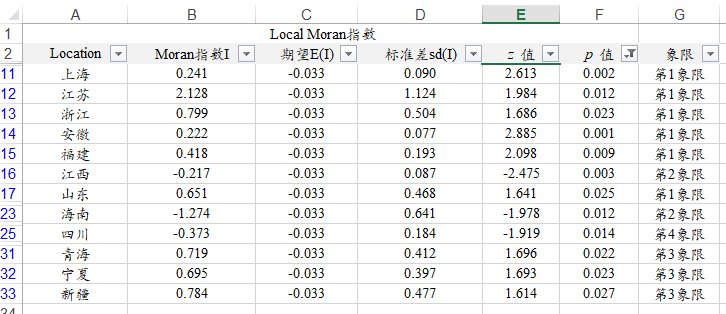
从上图可以看到,仅部分省市的Local Moran指数呈现出显著性。其中:上海,江苏,浙江,安徽,福建、山东,青海,宁夏,新疆这9个省呈现出显著性,而且这9个省份对应的Moran指数值均大于0,即意味着这9个省份具有空间正相关关系,也即说明该几个省份与其邻居省份之间具有正向协调关系,其GDP可能会带动周边省份的发展。与此同时,江西,海南,四川这3个省也呈现出显著性,但其Moran指数值小于0,即意味着该3个省呈现出空间负相关关系,该3个省的GDP发展反而会负面影响其邻居省份的GDP。
接着可进一步结合Local Moran指数的显著性,和其所属象限情况综合分析。
-
特别提示:
-
建议可选筛选出Local Moran指数呈现出显著性的对象深入分析;
-
结合Moran散点图可进一步了解研究对象的空间相关关系情况。
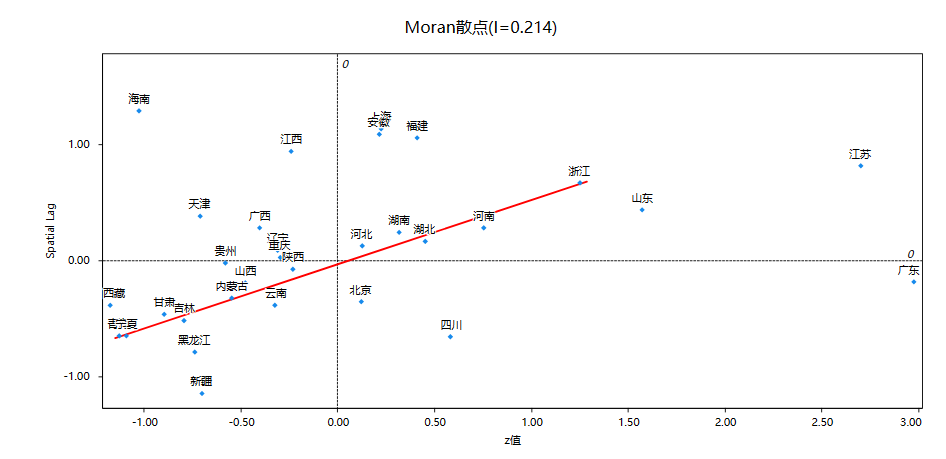
针对Moran散点图,X轴(离值z值)代表数据值与均值的距离,因而越靠右侧的数据意味着其GDP值相对越大,Y轴(Spatial Lag)表示空间滞后值,该值越大代表研究对象的邻居(周边)GDP值相对越大。结合实际意义可知4个象限的意义等如下表:
全局Moran指数 象限 相关性 意义 第1象限 空间正相关 高GDP和高GDP聚集 第2象限 空间负相关 低GDP和高GDP聚集 第3象限 空间正相关 低GDP和低GDP聚集 第4象限 空间负相关 高GDP和低GDP聚集 -
结合Local Moran指数的显著性可知:
-
上海,江苏,浙江,安徽,福建、山东这6个省,它们聚集在第1象限,意味着该6个省具有空间正相关关系,而且是高GDP与高GDP聚集关系;
-
青海,宁夏,新疆共3个省,它们聚集在第3象限,意味着该3个省具有空间正相关关系,但是它们均为低GDP与低GDP聚集关系;
-
江西和海南聚集在第2象限,意味着该2个省具有空间负相关关系,而且是低GDP与高GDP聚集关系;
-
四川在第4象限,意味着四川省具有空间负相关关系,而且是高GDP与低GDP聚集关系。
-
-
6、剖析
-
Moran指数分析涉及以下几个关键点,分别如下:
-
首先分析全局Moran指数,如果其呈现出显著性则可进一步分析Local局部Moran指数;
-
局部Moran指数呈现出显著性后,可进一步结合Moran散点图及其所属象限情况,深入挖掘和分析空间聚集关系情况。
-
疑难解惑
-
SPSSAU进行moran指数时提示‘权重矩阵需要对称!’?
-
Moran指数时,不论是邻接权重矩阵或距离权重矩阵,权重矩阵一定需要对称,即aij=aji,如果不是需要进行检查后重新输入。
-
MORAN指数下拉 标准化处理化方式参数说明 ?
-
MORAN指数时进行标准化处理是消除空间权重值的量纲尺度问题,正常情况下应该按行标准化,即每个值除以该行数据之和,这样每行求和为1,每个权重值的意义为相对距离大小。如果是按行列标准化,即每个数字除以全部权重值之和,这样全部空间权重矩阵数字加和1,其也进行量纲处理,但其实实际意义比较弱,其把值压缩到全部权重的占比,一般使用较少。与此同时,如果确定数据没有量纲问题也可以选择不进行量纲处理。
-
SPSSAU进行moran指数时文档上传空间权重矩阵是什么意思?
-
SPSSAU中进行moran指数分析时,空间权重矩阵支持粘贴上传和文档上传两种方式,粘贴上传最多支持100*100矩阵,文档上传可支持更多,文档上传时需要注意空间权重矩阵的数据格式,第1行是空间点的名称,从第2行起为n*n的矩阵(n表示空间点),将空间权重矩阵整理在EXCEL并且上传到SPSSAU中后,可下拉选择该数据文档作为附件参数传入让SPSSAU计算MORAN指数。