Heckman两阶段模型

•  分析方法视频解读： B站 优酷

• 案例数据下载 下载

Heckman两阶段模型案例

• 1、背景

  当前有一项关于薪资影响因素的研究，被解释变量薪资，解释变量为GRE成绩，但是会出现一个问题即薪资中有很多缺失数据（即样本偏差内生性问题），一种处理方式是直接过滤掉缺失数据进行分析，但这种分析方式仅仅是避开样本选择偏差内生性问题，如果要直面此种样本选择偏差内生性问题，则可考虑使用Heckman两阶段模型。除此之外，GPA成绩可能会影响到‘是否有薪资’数据，其可作为‘是否有薪资数据’的解释变量。为更加方便的查看被解释变量薪资的数据分布情况，将薪资作直方图如下：

  

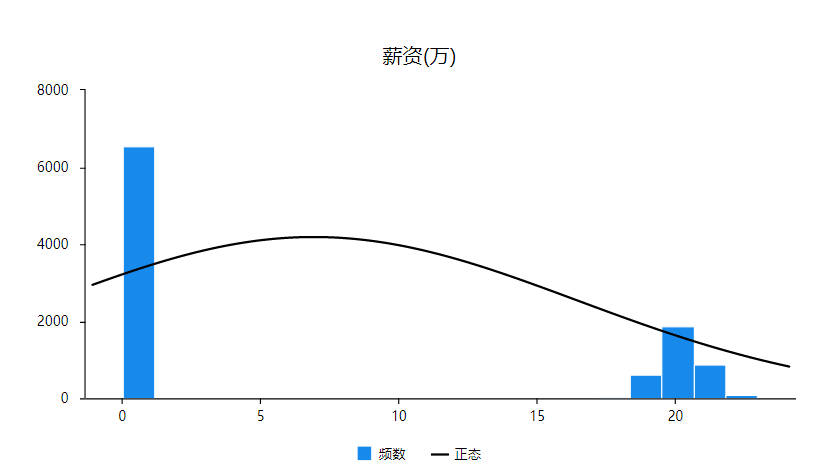
  从上图可以明显的看到，数字出现删失，即有一部分数据集中在数字0（数字0代表没有薪资数据，当然也可以使用null值表示，只是heckman两阶段模型时需要使用数字0表示没有该数据）。当然在分析的时候可考虑筛选出数字大于0的数据再进行ols线性回归也可（但这样做仅仅是避开样本选择偏差可能的内生性问题），如果说筛选出薪资大于0后再做直方图如下：

  

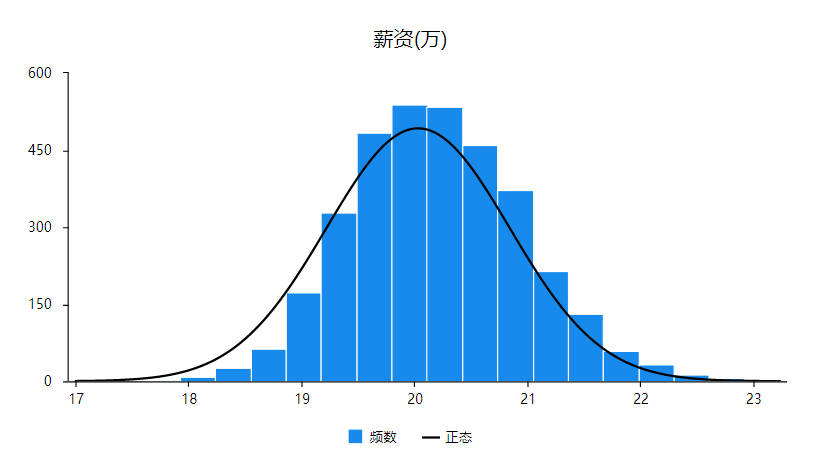
  明显的可以看到，筛选出薪资大于0的数据，其明显的服从正态分布，使用ols线性回归非常适合。但本案例使用heckman两阶段模型目的在于解决样本选择偏差导致样本的内生性问题。

• 2、理论

  Heckman两阶段模型时，被解释变量（因变量）Y有着缺失数据，通常首先需要将被解释变量设置为0和1，0代表删失（即没有该项数据），1代表未删失（即有该项数据），得到新的变量，比如本案例为‘薪资(0代表无1代表有）’，其共分为两个阶段，说明如下：

  √  第1阶段：二元probit回归模型；即将薪资(且为01项二元数据)作为被解释变量，并且纳入解释变量（一般情况下，解释变量为核心研究解释变量与工具变量），进行二元probit模型后，得到IMR值（Inverse Mill's Ratio）。

  √  第2阶段：ols回归模型，将‘薪资’作为被解释变量，并且模型会自动纳入第1阶段得到的IMR值，以及研究的核心解释变量进行分析，并且在第2阶段分析时，会自动过滤出‘未删失’即薪资没有缺失的数据，并且得到结果。

  √  针对分析上：如果IMR值呈现出显著性(p<0.05)，即意味着存在样本偏差内生性问题，也即说明有必要使用Heckman两阶段模型进行分析，反之如果IMR值没有呈现出显著性(p>0.05)，即意味着样本偏差内生性问题不严重（或不存在），此时可考虑使用 Heckman两阶段模型（或者ols回归均可）。

  √  另heckman两阶段模型分析上依旧是针对解释变量的显著性进行分析即可，并无其它特别点，其核心应用为处理样本选择偏差带来的内生性问题。

• 3、操作

  本案例操作截图如下：

  

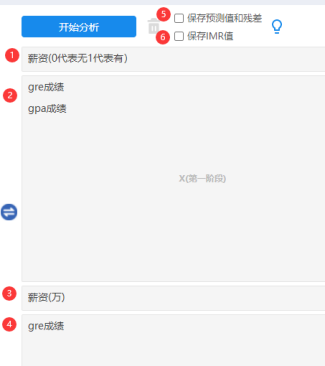
  项	名称	说明
  1	Y1(第1阶段,01变量)	第1阶段二元probit回归的被解释变量，其只能为0和1两个数字。本案例为‘薪资(0代表无1代表有)’。
  2	X(第1阶段)	第1阶段二元probit回归的解释变量，本案例为‘GPA成绩’和‘GRE成绩’。
  3	Y2(第2阶段,定量)	第2阶段ols回归的被解释变量，本案例为‘薪资(万)’。
  4	X(第2阶段)	第2阶段ols回归的解释变量，本案例为’gre成绩’。
  5	保存预测值和残差	选中后，系统会自动生成新标题，用于存储第1阶段和第2阶段的预测值和残差，共4项。
  6	保存IMR值	选中后，系统会自动生成新标题，用于存储第1阶段后计算得到的IMR值，共1项。

  • 特别说明：

  • 第1阶段的Y1即01二元数据，其为第2阶段的Y2进行数据编码得到，可使用数据处理->数据编码功能处理，数字0代表删失（即没有薪资数据），数字1代表未删失（即有薪资数据）；

  • 本案例时第1阶段和第2阶段的X中，都有‘gre成绩’，二者完全一样，如果上传数据仅1项，此时可通过数据处理->生成变量功能里面的平均值功能(自己平均就是自己)，复制一个完全相同的数据；

  • 本案例时第1阶段中有2个X，分别是‘gre成绩’和‘gpa’成绩，该两项可能影响到‘是否有薪资’数据，所以纳入该两项，具体应以实际研究为准即可；

  • 通常情况下并不需要保存预测值和残差，也或者IMR值。

• 4、SPSSAU输出结果

  SPSSAU共输出6类表格，分别说明如下：

  表格名称	说明
  Heckman两阶段模型模型汇总	Heckman两阶段模型的基本描述，包括被解释变量和解释变量的列出。
  研究数据基本汇总	删失数据或缺失数据的具体情况展示等。
  第1阶段（二元Probit回归）分析结果汇总	第1阶段二元probit回归模型的结果汇总。
  第2阶段（OLS回归）分析结果	第2阶段ols回归模型的结果汇总。
  第1阶段(二元Probit回归)分析结果汇总-简化格式	第1阶段二元probit回归模型的简化结果汇总。
  第2阶段（OLS回归）分析结果-简化格式	第2阶段ols回归模型的简化结果汇总。

• 5、文字分析

  

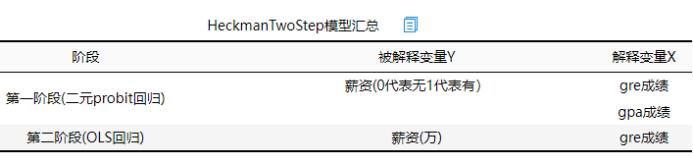
  上表格展示Heckman两阶段模型基本情况，包括第1阶段和第2阶段时，分别对应的被解释变量和解释变量情况。

  

  上表格展示Heckman两阶段模型研究数据基本情况，针对第1阶段的被解释变量薪资中有6548个删失数据（即数字为0的个数），3452个未删失（即数字为1的个数）。以及数据中没有其它缺失数据。

  

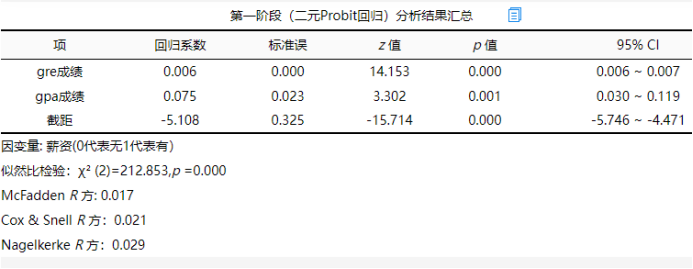
  上表格展示第1阶段二元probit回归的结果，包括模型的R方值，似然比检验，各解释变量的显著性情况等，事实上第1阶段二元probit回归结果的意义较小(多数时候并不关注R方，似然比检验，显著性等指标)，因为第1阶段二元probit回归目的在于计算得到IMR值，纳入第2阶段OLS回归中。上表格中gre成绩和gpa成绩均呈现出0.01水平显著性，意味着该两项确实会影响到‘是否有薪资数据缺失’。

  

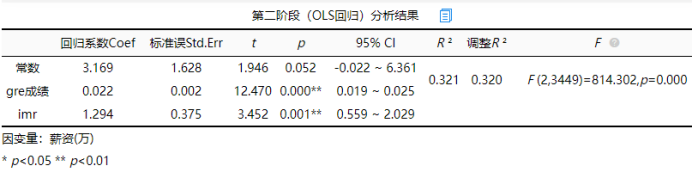
  上表格展示出Heckman第2阶段ols回归结果，表格中默认包括IMR值，其为第1阶段回归得到的中间过程值。如果IMR值呈现出显著性(p<0.05)，即意味着存在样本偏差内生性问题，也即说明有必要使用Heckman两阶段模型进行分析；如果IMR值没有呈现出显著性(p>0.05)，即意味着样本偏差内生性问题不严重（或不存在），此时可考虑使用 Heckman两阶段模型（或者ols回归均可）。

  从上表可知，IMR值并呈现出显著性(p=0.001)，也即意味着存在样本偏差内生性问题，也即说明有必要使用Heckman两阶段模型进行分析,接下来具体分析：gre成绩的回归系数值为0.022，p值为0.000，小于0.01，意味着gre成绩会对薪资(万)产生显著的正向影响关系。

  总结分析可知：gre成绩会对薪资产生显著的正向影响关系，也即说明gre成绩越高时，薪资也会越高。

  

  上表格展示出Heckman第1阶段二元probit回归的简化结果表格，该表格列出模型的关键信息点，可直接使用。

  

  上表格展示出Heckman第2阶段ols回归的简化结果表格，该表格列出模型的关键信息点，可直接使用。

• 6、剖析

  涉及以下几个关键点，分别如下：

  • 提示‘Y值只能为0或1’，第1阶段二元probit回归时，被解释变量Y只能包括数字0和1，数字0代表未删失，数字1代表删失。

• 7、疑难解惑

  • heckman两阶段模型的原理？

  • Heckman两阶段数学模型分为两阶段，第1阶段为二元probit模型，并且得到IMR值，第2阶段为ols回归，且模型中默认包括第1阶段中的IMR值，以及第2阶段的解释变量。第1阶段时的被解释变量（因变量）Y只能包括数字0或1，第2阶段ols回归时其样本量为过滤掉第1阶段Y为1（即未删失）的样本量。

  • heckman两阶段模型时第1阶段和第2阶段的被解释变量(因变量)Y是否一致？

  • 通常情况下，第1阶段和第2阶段的被解释变量(因变量)Y意义均一致，但数字不一致，第1阶段的Y时数字只能为0或1，意义为0代表样本缺失1代表样本存在，第2阶段的Y时数字代表其真实意义。简而言之，第1阶段的Y通常情况下是由第2阶段的Y进行处理后得到。

  • IMR值的意义？

  • IMR是一个用于修正样本选择偏差的值，其是在heckman两阶段模型的第一阶段计算得到。

  • IMR值是否显著的意义？

  • 如果IMR值显著，此时说明样本偏差问题存在，也即说明使用heckman两阶段模型进行样本选择偏差纠正是适合的并且且有必要。反之如果IMR值不显著，此时可能意味着模型不存在严重的样本选择偏差，那么也即说明第二阶段模型的结果应该与普通ols回归的结论基本一致，研究者可使用spssau计量模块里面的ols回归进行分析对比使用，也即说明IMR值不显著时，一般使用ols回归或者heckman两阶段模型均可。

  • heckman两阶段模型时第1阶段的解释变量X应该包括那些变量？

  • 一般情况下第1阶段模型中的解释变量应该以‘可能影响到样本偏差项的变量’为主。具体应以研究者思路为准，spssau系统中第一阶段和第二阶段中的解释变量X可完全分开放置。

  • heckman两阶段模型时第2阶段的解释变量X应该包括那些变量？

  • 第2阶段中的解释变量为核心研究解释变量，直接放入即可。

  • heckman两阶段模型时同一变量不同放入2个框中？

  • heckman两阶段模型时第1阶段或第第2阶段时，可能会放入完全相同的变量，但一个变量只能放入1个框中。建议可先使用‘数据处理->生成变量‘的平均值功能，先得到1个新的并且数据完全相同的变量即可，也或者上传数据时就有两个完全相同的变量项。