误差修正ECM模型案例

• 1、背景

  当前有一项美国宏观联邦基金利率、通货膨胀率和失业率的数据，数据日期从1960年第1季度到2012年第1季度，单位为季度，共计209个数据。现针对该3个宏观计量研究进行研究时发现该3项满足同阶单整（1阶单整）（可参考SPSSAU中VAR模型或coint协整的手册），并且通过协整检验，本案例使用误差修正模型ECM研究短期波动情况。（数据序列满足1阶差分平稳，因此误差修正模型ECM时也使用1阶差分后数据）。部分原始数据如下图所示：

  

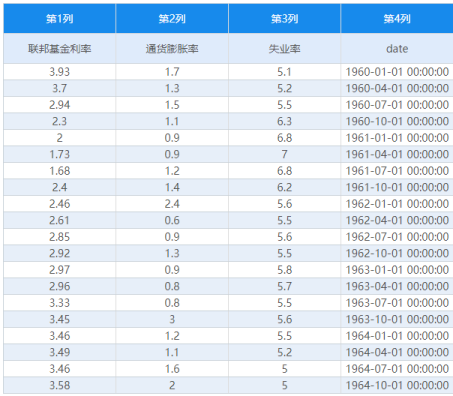
• 2、理论

  SPSSAU中误差修正ECM模型为EG两步法（EG-ADF法）， EG两步法原理，如下述说明：

  1、 先建立X和Y的ols线性回归，并且得到残差resid（也称为ECM）；

  2、 将Y，X分别取差分1阶，得到detY，detX，并且将ECM取滞后一阶即ECM(-1)；

  3、 建立detY，detX，ECM(-1)的ols线性回归。

  关于误差修正模型的分析使用流程，可参考下图：

  

  1)原序列不平稳且同阶单整，先做协整检验；

  2)如果拒绝原假设，即有协整关系说明长期均衡关系，可进一步ECM检验短期关系；

  3)如果无法拒绝原假设，即没有协整关系说明没有长期均衡关系，不能使用ECM模型检验短期关系。

  • 特别提示：

  • 协整检验研究长期均衡稳定关系，但在短期中，这种关系可能偏离均衡，它需要一种机制来表其对短期失衡的修正。那么意味着误差修正ECM模型的构建，通常是在满足前期条件（即满足协整关系）时才能进一步使用；

  • 协整关系的研究是针对同阶单整数据，那么意味着原始序列数据有单位根不平稳，而同阶差分后数据平稳，那么进行ECM模型构建的时候也需要使用差分后的数据（提示：协整关系检验时是使用原始序列数据）。

• 3、操作

  本例子数据时在前期构建VAR模型（或协整检验）时发现1阶差分平稳，因此进行误差修正ECM模型时也先对数据一阶差分，1阶差分的设置在SPSSAU数据处理->生成变量中，如下图所示：

  

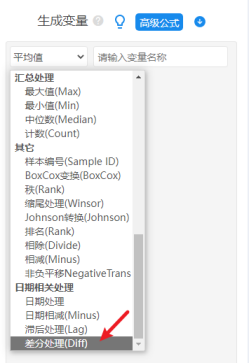
  分别针对3个研究变量进行1阶差分，得到3个新标题如下：

  

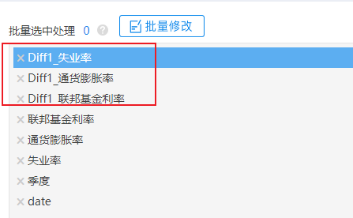
  接着使用新的3个差分1阶变量进行误差修正ECM模型，关于误差修正ECM模型的操作截图如下：

  

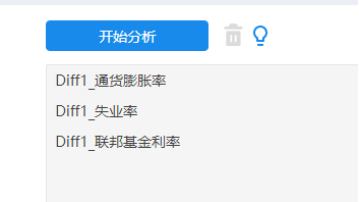
  放入分析框中的第1项即为Y（本案例为通货膨胀率），余下的2项为X（本案例分别是失业率和联邦基金利率）。当然研究者可以自行更换分析项放入顺序来更换X和Y。

• 4、SPSSAU输出结果

  关于ECM模型时，SPSSAU输出2个表格，说明如下：

  名称	说明
  协整回归模型结果	协整回归模型研究长期均衡关系
  误差修正ECM模型结果	ECM模型研究短期波动关系情况

• 5、文字分析

  

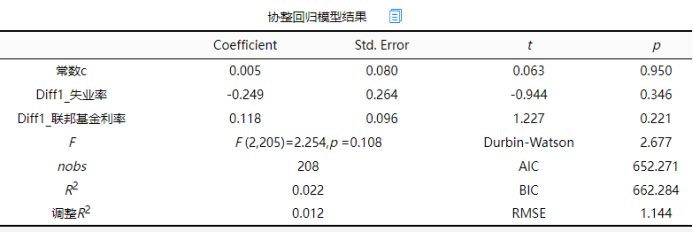
  协整回归模型研究长期均衡关系，从上表可以看到：协整方程模型公式为：通货膨胀率=0.005-0.249*失业率 + 0.118*联邦基金利率。长期均衡关系的检验上看，失业率的系数值为-0.249，并没有呈现出显著性(t =-0.944,p =0.346>0.05),意味着失业率不会对通货膨胀率产生长期影响关系。

  联邦基金利率的系数值为0.118，并没有呈现出显著性(t =1.227,p =0.221>0.05),意味着联邦基金利率不会对通货膨胀率产生长期影响关系。

  • 特别提示：

  • 误差修正ECM模型(EG两步法)，其提供协整回归模型和误差修正ECM模型。一般情况下，更加关注于后者即误差修正ECM模型。而长期关系，通常是通过协整模型进行分析，因而上述表格中即使没有呈现出显著性，通常情况下也没有关系。

  • 除此之外，还可分别更换失业率、联邦基金利率作为Y，另外2个作为X，分别重复进行分析汇总结果。

  

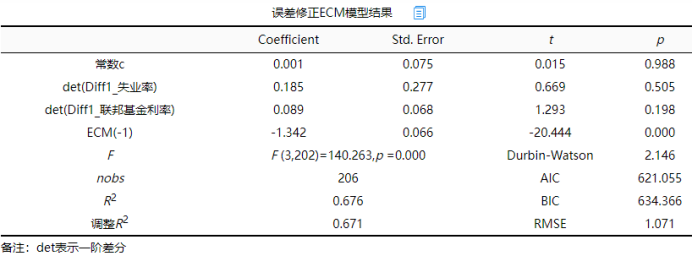
  上表格展示误差修正ECM模型结果。Det这个符号表示差分一阶的意思，ECM(-1)为协整回归模型中得到的残差差分项，其表示上期误差值。分析角度来看：

  如果序列1阶差分项呈现出显著性，则说明该序列当期波动会对Y当期波动调整幅度，反之说明可能该序列当期波动不会对Y当期波动产生调整影响；

  如果上期误差值ECM(-1)系数即修正系数呈现出显著性，则说明短期波动偏离长期均衡即非均衡状态时，上期误差ECM(-1)会将该非均衡状态拉回到均衡状态水平(即对非均衡状态进行调整)，反之则说明上期误差对非均衡状态的调整幅度不大。

  针对本案例来看：首先ECM模型公式为：通货膨胀率=0.001 + 0.185*det(失业率) + 0.089*det(联邦基金利率)-1.342*ECM(-1)。从模型检验上看，ECM模型通过F检验(F =140.263，p =0.000<0.1)，意味着ECM模型构建良好。

  针对短期波动影响情况上，失业率差分项的系数值为0.185，并没有呈现出显著性(t =0.669,p =0.505>0.05),意味着失业率不会对通货膨胀率当期波动带来短期波动均衡调整。

  联邦基金利率差分项的系数值为0.089，并没有呈现出显著性(t =1.293,p =0.198>0.05),意味着联邦基金利率不会对通货膨胀率当期波动带来短期波动均衡调整。

  误差修正系数值为-1.342，呈现出0.01水平显著(t =-20.444,p =0.000<0.01),意味着当短期波动偏离长期均衡时,将以-1.342（134.2%）的调整力度将非均衡状态拉回到均衡状态。

• 6、剖析

  • 涉及以下几个关键点，分别如下：

  • 协整检验研究长期均衡稳定关系，但在短期中，这种关系可能偏离均衡，它需要一种机制来表其对短期失衡的修正。那么意味着误差修正ECM模型的构建，通常是在满足前期条件（即满足协整关系）时才能进一步使用。

  • 协整关系的研究是针对同阶单整数据，那么意味着原始序列数据有单位根不平稳，而同阶差分后数据平稳，那么进行ECM模型构建的时候也需要使用差分后的数据（提示：协整关系检验时是使用原始序列数据）。

  • SPSSAU提供EG两步法误差修正模型，其提供两个模型分别是协整回归模型和误差修正ECM模型结果，前者研究长期均衡关系，后者研究短期波动关系。通常情况下长期均衡是使用协整检验进行研究，因而分析上多数情况下更加关注于后者（即ECM模型研究短期波动关系）。