ARIMA模型分析

ARIMA模型（移动平均自回归模型），其是最常见的时间序列预测分析方法。利用历史数据可以预测前来的情况。ARIMA模型可拆分为3项，分别是AR模型，I即差分，和MA模型。SPSSAU智能地找出最佳的AR模型，I即差分值和MA模型，并且最终给出最佳模型预测结果，SPSSAU智能找出最佳模型的原理在于利用AIC值最小这一规则，遍历出各种可能的模型组合进行模型构建，并且结合AIC最小这一规则，最终得到最佳模型。

当然，研究人员也可以自行设置AR模型，差分阶数和MA模型，即分别设置自回归阶数p，差分阶数d值和移动平均阶数q，然后进行模型构建。至于自回归阶数p，差分阶数d值和移动平均阶数q值应该设置多少合适，建议研究人员分别使用偏(自)相关图进行分析（SPSSAU也智能提供p值或q值建议），以及使用ADF检验分析得出合适的差分阶数d值（SPSSAU也智能提供最佳差分阶数d值建议）。

    特别提示

  • SPSSAU默认智能地找出最佳的ARIMA模型并且进行预测。

  • 如果研究人员自己设置自回归阶数p，差分阶数d值和移动平均阶数q这3个参数，SPSSAU则按照研究人员设置进行模型构建。

ARIMA模型案例

  • 1、背景

    当前已经有阿里“双十一”历年（2009~2019年）的销售数据，现希望通过历史数据预测2020年阿里“双十一”的销售额情况。数据如下：

    年份 阿里双十一销售额（亿元）
    2009 0.5
    2010 9.36
    2011 52
    2012 191
    2013 350
    2014 571
    2015 912
    2016 1207
    2017 1682.69
    2018 2135
    2019 2684
      特别提示

    • 时间序列的数据格式上，一定是时间从上至下递增，而且不能有间隔，比如2015，2017，2018这种数据少了2016，这类数据不能称为时间序列数据。

    • 时间序列的单位一般是年，比如我国历年的GDP数据，也或者我国历年人口数据等。当然如果单位是月或者季度，也或者周等，可以体现出数据的变化规律，也一样可以作为时间序列数据使用。

  • 2、理论

    ARIMA模型可拆分为3项，分别是AR模型，I即差分，和MA模型。SPSSAU智能地找出最佳的AR模型，I即差分值和MA模型。当然，研究人员如果自行设置AR模型，差分阶数和MA模型，即分别设置自回归阶数p，差分阶数d值和移动平均阶数q，此时SPSSAU则按照研究人员的设置进行模型构建。建议用户直接使用SPSSAU的智能分析即可。

  • 3、操作

    本次研究希望SPSSAU自动拟合出最佳的ARIMA模型，因此不设置3个参数（自回归阶数p，差分阶数d值和移动平均阶数q）。操作如下图：

  • 4、SPSSAU输出结果

    SPSSAU共输出4个表格，第1个表格是拟合模型参数表格（即SPSSAU拟合出的最佳模型表格），如果研究人员自行设置了参数，则按照研究人员设置的模型进行构建。第2个表格是模型残差Q统计量检验表格，第3个表格是模型预测值（共往后12期的模型预测值），第4个表格是模型残差LM检验。

    同时SPSSAU还输出模型拟合、预测的折线图，便于直观展示拟合效果和预测情况。如果研究者需要原始的残差或拟合值，可点击‘开始分析’按钮右侧‘保存残差和预测值’，系统会自动新生成2个标题用于标识残差和预测值。

  • 5、文字分析

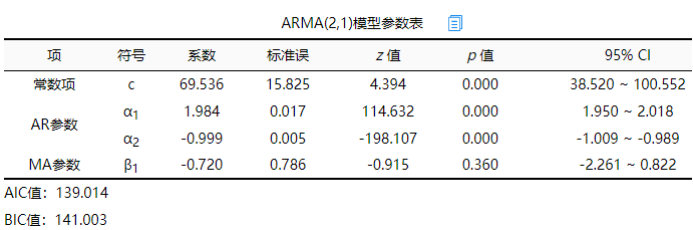
    上表格展示本次模型构建结果，包括模型参数和信息准则。本次模型构建时，SPSSAU自动构建出模型为：ARMA(2,1)，其模型公式为：y(t)=69.536+1.984*y(t-1)-0.999*y(t-2)-0.720*ε(t-1)。如果研究人员希望自己进行模型构建并且进行优劣对比，可先记录下每个模型的AIC或BIC值，然后结合AIC或BIC值越小越好的原则，选择最优模型。

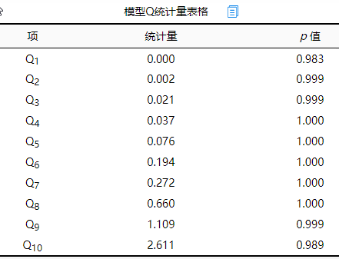
    除此之外，SPSSAU还输出Q统计量值，AIRMA模型构建后一般要求模型残差为白噪声，即残差不存在自相关性，可通过Q统计量检验进行白噪声检验（原假设：残差是白噪声）；比如Q6用于检验残差前6阶自相关系数是否满足白噪声，通常其对应p 值大于0.1则说明满足白噪声检验（反之则说明不是白噪声），常见情况下可直接针对Q6进行分析即可；从Q统计量结果看，Q6的p 值为1.000大于0.1，则在0.1的显著性水平下不能拒绝原假设，模型的残差是白噪声，模型基本满足要求。

    上表格预测值表格研究者最关心的表格，因为ARIMA模型目的就在于预测以后的数据情况。向后1期即指2020年，向后2期是指2021年的数据。从经验上看，ARIMA模型向后预期的1期和向后2期相对较为可靠，如果向后期数过多，则准确性会较低。建议研究人员更多参考向后1期或向后2期的数据。即本次利用阿里“双十一”历年（2009~2019）的数据进行预测，使用ARIMA模型进行预测，最终预测出阿里“双十一”2020年的销售额应该为3225.968亿元。

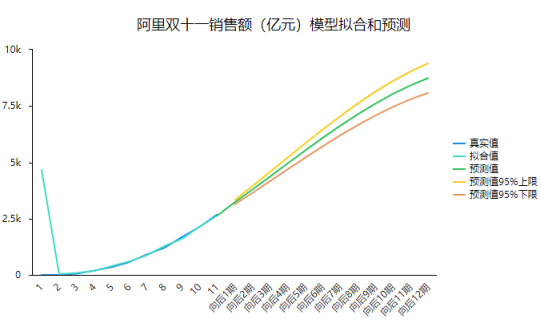
    SPSSAU默认展示时间序列最近1000期的实际值和拟合值、以及最近12期数据预测数据。从上图可以看到，真实数据和拟合数据基本上完全吻合，也即说明模型拟合非常好。而且整体上看，模型预测值呈现出缓慢增长的趋势。

      提示

    • 如果原始数据>1000条,此时希望查看全部的拟合值，可点击‘开始分析’按钮右侧‘保存残差和预测值’，系统会自动新生成2个标题用于标识残差和预测值。

    • 默认向后预期12期，如果希望改变，可修改‘向后预测期数’这个参数即可

  • 6、剖析

    涉及以下几个关键点，分别如下：

    • SPSSAU默认智能地找出最佳的ARIMA模型并且进行预测（智能拟合模型的原理在于利用AIC值越小越好这一规则，从众多潜在的模型中进行对比选择出最佳模型）。

    • 如果研究人员自己设置自回归阶数p，差分阶数d值和移动平均阶数q这3个参数，SPSSAU则按照研究人员设置进行模型构建。

    • SPSSAU自动提供未来12期的预测数据，但针对ARIMA模型来讲，一般情况下未来1期或者未来2期的预测较为准确，更远的预测数据预测准确率较低，通常作为参考即可。

    • 如果数据具有周期性波动，而且比较规律，则需要使用SARIMA模型。

疑难解惑

  • Arima预测当前帮助手册与分析结果不一致？

  • SPSSAU于2021.8月对arima模型进行升级，升级后的算法有所改变，当前帮助手册中的结果会有较大变化。

  • SPSSAU中arima模型时Q统计量？

  • SPSSAU进行arima模型分析时，默认输出Q统计值及其p值，Q统计量用于检验模型残差是否满足白噪声。研究者也可先让arima模型保存预测值和残差，然后针对残差进行偏自相关图即可。

  • SPSSAU中arima模型时LM检验？

  • SPSSAU进行arima模型时，默认提供残差拉格朗日乘数检验(Breush-Godfrey LM检验)，该检验用于检验模型残差序列是否存在序列相关，该检验可能有助于后续其它模型的使用判断，比如ARCH模型。

  • SPSSAU中arima模型保存拟合值？

  • SPSSAU进行arima模型时，可选中开始分析按钮右侧‘保存残差和预测值’参数，系统会自动新生成两个标题来标识对应的预测值和残差，另提示，如果实际拟合的模型有着差分项，此时输出的残差或拟合值的前d项会缺失(d代表差分阶数)。

  • SPSSAU进行arima预测时的RMSEA指标意义？

  • RMSEA的意义为残差平方和的平均值并且开根号，即平均的残差值情况，SPSSAU默认输出该指标值。

  • SPSSAU进行arima预测时提示‘样本量过大请使用手工建模！’？

  • 如果样本量>1万,此时不提供智能识别模型,可自行设置pdq等参数值后构建arima预测。

  • RMSE、MSE、MAE和MAPE这4个指标分别什么意义？

  • RMSE（均方根误差），其表示模型拟合后的平均残差情况如何，即模型拟合后真实值与预测值之间的偏差有多大，该值越小越好；

  • MSE(均方误差)，其表示模型拟合后的平均残差平方值如何，MSE开根号即为RMSE值，该值越小越好；

  • MAE（平均绝对误差），其为残差的绝对值之和，然后求平均值，其表示平均偏差是多大，与RMSE的意义基本一致，该值越小越好；

  • MAPE（平均绝对百分比误差），其为残差除以真实值的绝对值之和，然后求其平均。该值为相对指标值，其表示预测值与真实值之间gap平均偏离真实值的比例情况，比如为0.2，其表示平均偏离真实值20%左右，该值越小越好，并且该指标值具有比较意义，不同模型之间均可对比该值的相对大小，进而衡量模型优劣情况。