相关分析用于研究两两变量之间的关系情况,如果有第三个变量,它会影响到这种关系情况,从而导致相关系数无法真实有效地反映变量间的关系情况,比如研究身高与肺活量之间的关系,是否身高越高,肺活量越大呢?如果直接进行相关分析,会出现有相关关系,但真实结论很可能并不应该这样,同样身高的人肺活量很可能明显不一样,原因是体重并不一样。身高与体重有相关性,而肺活量也与体重有相关性。因此研究身高与肺活量的关系时,体重会有干扰作用,因此在研究时应该将体重作为控制变量,以防止其干扰。类似这样的相关关系研究,就应该使用偏相关分析。
另外如果研究工资与受教育年限的关系时,年龄和工作经验也应该是控制变量,因为年龄和工作经验,分别均与工资或受教育年限之间有着相关关系。类似这样的研究时,均需要使用偏相关分析(将控制变量纳入考虑范畴内),才能得到更加科学的结论。
-
提别提示
-
控制变量是指同时与相关分析的两个变量,很可能均有着相关关系的变量。
偏相关分析案例
-
1、背景
当前某研究人员想研究员工受教育年限与当前工资之间的关系,以及每个员工的入职工资会起着干扰作用,入职工资与受教育年限有关系,同时入职工资与当前工资也有着相关关系。受教育年限会影响入职工资,入职工资还会影响到当前工资。因此研究受教育年限与当前工资的相关有关系时,需要将入职工资作为控制变量纳入考虑范畴内。
-
2、理论
偏相关分析是在相关分析基础上,进一步考虑干扰因素时使用的研究方法。此干扰因素,也称其为“控制变量”,控制变量一般与相关分析的变量之间均有着相关关系,如果控制变量与相关分析的变量之间并没有关系,那么就不会有干扰作用。SPSSAU在偏相关分析输出结果时,默认会输出控制变量分别与相关分析变量之间的相关关系系数,便于考察某项是否为真正的控制变量。
如果明知道某项具有干扰作用但是不作控制,可能无法得到科学的结论。
-
3、操作
-
本例子研究当前工资与受教育年限的关系情况,将入职工资作为控制变量纳入分析中,便于控制入职工资对分析的干扰影响。操作如下图:
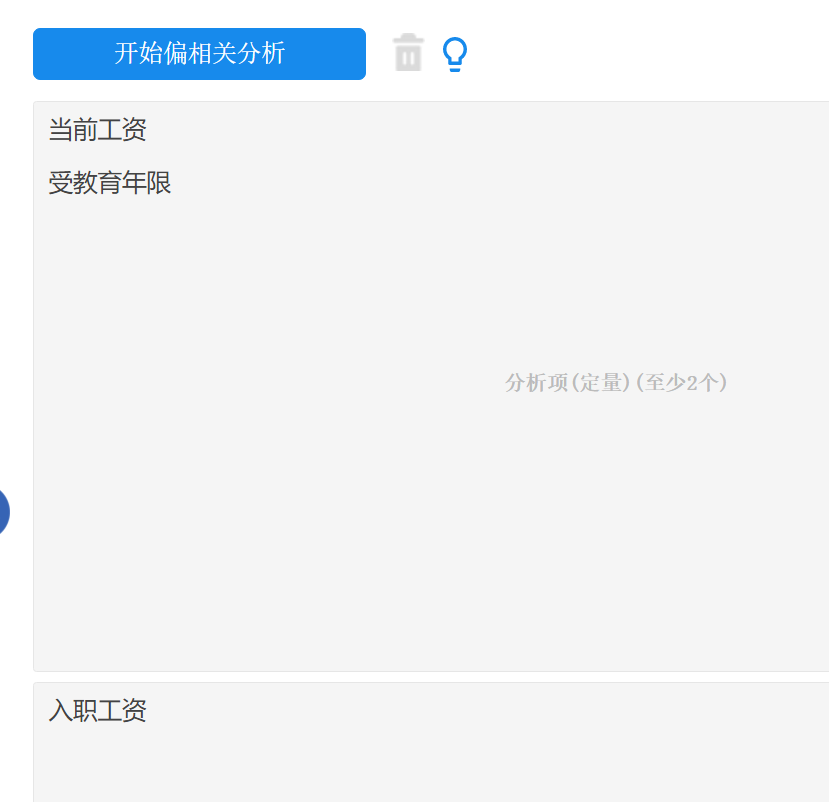
-
-
4、SPSSAU输出结果
SPSSAU共输出2个表格,分别是研究变量之间的相关关系,控制变量与研究变量之间的相关关系表格,分别如下:
偏相关分析结果 平均值 标准差 当前工资 受教育年限 当前工资 36471.750 18634.744 1 受教育年限 13.765 2.818 0.327** 1 * p < 0.05 ** p < 0.01 分析项和控制变量相关分析结果 当前工资 受教育年限 入职工资 0.894** 0.624** * p < 0.05 ** p < 0.01 -
5、文字分析
偏相关分析结果 平均值 标准差 当前工资 受教育年限 当前工资 36471.750 18634.744 1 受教育年限 13.765 2.818 0.327** 1 * p < 0.05 ** p < 0.01 本次研究工资与受教育年限之间的与受教育年限的关系情况,将入职工资作为控制变量纳入分析中,便于控制入职工资对分析的干扰影响。从上表可以看出,当前工资与受教育年限之间的相关系数为0.327,并且呈现出0.01水平的显著性(p < 0.01),说明二者之间有着比较紧密的正向相关关系。
分析项和控制变量相关分析结果 当前工资 受教育年限 入职工资 0.894** 0.624** * p < 0.05 ** p < 0.01 从上表可以看到:入职工资与当前工资之间有着非常紧密的正相关关系,相关系数值高达0.894,而且入职工资与受教育年限之间的相关系数值为0.624,说明二者之间有着紧密的正向相关关系。也即说明入职工资分别与当前工资,受教育年限之间有着紧密的正相关关系,入职工资作为控制变量纳入分析中较为合适,并且起到控制作用。
-
特别提示
-
本例子中,如果不将入职工资作为控制变量纳入考虑范畴内,而直接进行相关分析,显示为:当前工资与受教育年限之间的相关系数值为0.672(非常紧密的正相关关系),明显高于偏相关分析时的0.327(一般相关),本身受教育年限与当前工资之间的相关关系一般,但是却显示为非常紧密的相关关系,结论不准确。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
控制变量是指同时与相关分析的两个变量,很可能均有着相关关系的变量;
-
如果明知道某项具有干扰作用但是不作控制,可能无法得到科学的结论。
-
