-
如果数学模型为非线性关系,比如人口学增长模型Logistic(S模型),其模式公式为:y = b1 / (1 + exp(b2 + b3 * x)),其中y为人口数量,x为年份(实际数据为第n年,数字从0年起,依次顺序增加),b1,b2和b3分别为三个估计参数,exp为自然指数的意思。此数学表达式并非线性表达式,因此不能使用SPSSAU的线性回归进行拟合。
诸如此类非线性关系(即不是直接关系)的非线性模型,可使用非线性回归进行研究。SPSSAU当前提供约50类非线性函数表达式,涵盖绝大多数非线性函数表达式。如下图:

-
备注:图中出现的b1,b2,b3等代表待估计参数;exp表示自然指数,ln表示自然对数,cos表示余弦函数;“**”表示指数的意思。
进行非线性回归模型构建时,通常分为三步。
第一步:首先需要结合专业知识选择正确的构建模型,比如人口增长预测时使用logistic模型,经济学研究的抛物线二次曲线模型等。
第二步:设置参数初始值;与线性回归不同,非线性回归模型数学原理上使用迭代思想计算参数估计值,因而对初始值的不同设置,很可能会导致不同的结果,因而初始值设置较为重要,其可使用模型求解更为精确,并且有助于模型快速迭代收敛。关于初始值的设置在案例中有更详细说明。
第三步:模型预测。在得到参数拟合值后,并且拟合效果在认可范围内时,那么可使用模型进行预测数据,输入X的数据信息,对应得到Y的预测值。
-
特别提示:
-
关于初始值。初始值是由研究人员输入的一个‘大概’值,即参数的大概估计值,大概预期的值,与此同时,也可设置参数的范围,即上下界,但通常情况下不设置上下界值,除非认为有必要,通常不需要设置上下界值。
-
关于初始值的设置方法。通常包括两种,一是结合专业知识进行判断,二是利用模型公式时的特殊点(比如X=0时,Y=?)去求解得到。专业知识判断上,某参数的实际意义为数据的最大值,那么就设定该参数为最大值即可。SPSSAU默认以数字1作为参数值。
-
NLS非线性回归模型案例
-
1、背景
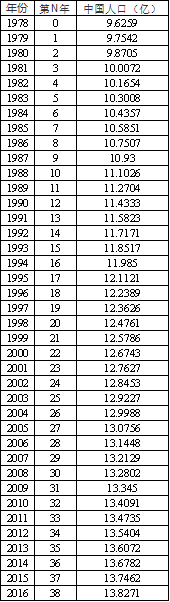
1978~2016共计39年我国人口数据,当前希望建立人口数量logistic模型(S模型),通常建立人口数量模型后,可为人口数据预测提供建议。案例数据如下:
-
2、理论
Logistic模型函数表达式为:y = b1 / (1 + exp(b2 + b3 * x)),其中y为人口数量,x为‘第N年’(起始1978年为数字0,1979为数字1,依次下去),b1,b2和b3分别为三个估计参数,exp为自然指数的意思。其中b1的实际意义为渐近线,即Y(人口)无限接近的数字。
自然的想到,人口最多在14亿左右,因而b1的初始值可设置为数字14。至于b2和b3这两个参数值,代入特殊点,即第0年,即x=0时,y=9.6259,可先计算出b2值为-0.79,接着基于b1,b2,b3,并且代入第1年这一特殊点数据,计算得到b3约为-0.042,因此就得到3个参数对应的初始值。当然不进行设置也可以,并没有固定要求,如果不设置,SPSSAU默认以数字1作为初始值,如果不设置,有可能出现计算结果不理想。
x值(第N年) 使用第0年和第1年这两个特殊点 y(人口) 第0年时,人口为9.6259;第1年时人口为9.7542 参数b1 结合专业知识设置为14 参数b2 9.6259=14/(1+exp(b2),计算后得到b2约等于-0.79 参数b3 基于b1=14,b2=-0.79,以及第1年即1979年数据(x=1,y=0.7542);即有9.7542=14/(1+exp(-0.79+b3),计算得到b3= -0.042 -
特别提示:
-
初始值的设置上并不固定要求,通常可结合模型的实际意义和实际数据情况进行设置,比如本案例中最大人口数量为14亿;与此同时,还可结合数据特殊点的特殊特征代入计算得到一个大概的初始值;比如本案例时分别代表x为0或1这两个特殊点,分别计算得到参数的初始值。
-
如果不设置初始值,SPSSAU默认以数字1作为初始值。
-
-
3、操作
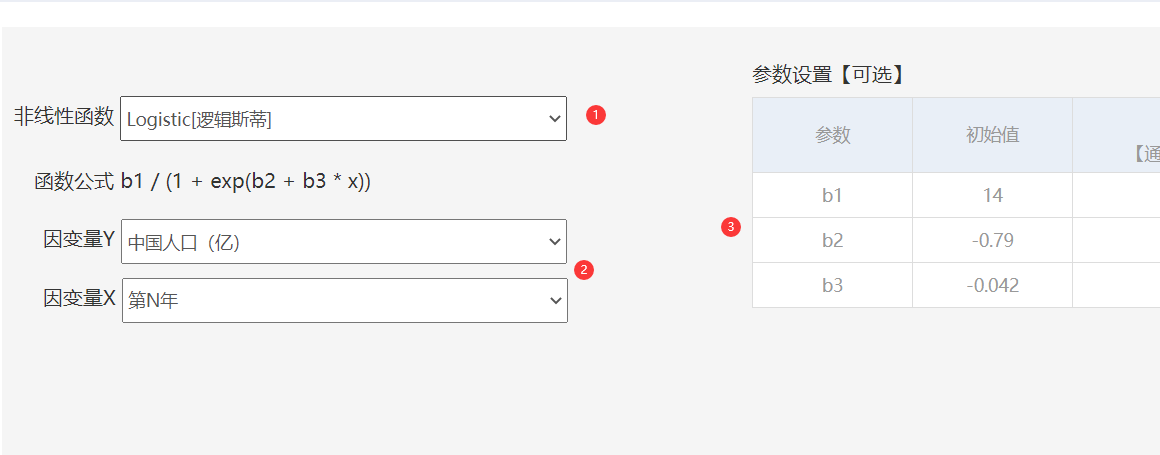
本例子SPSSAU操作截图如下:
-
注意如下:
-
首先选择正确的非线性函数(即模型),函数公式处会展示出该模型对应的函数公式(即模型表达式),选择对应的因变量和自变量数据,设置好参数后点击分析即可。
-
参数的初始值上,如果没有把握,一般直接不设置就好,但建议针对初始值进行设置;
-
参数的上下界通常不需要进行设置,除非有较大的把握。比如本案例的人口初始值为14亿,那么下界可设置为10,上界可设置为20。
-
-
4、SPSSAU输出结果
SPSSAU输出3个表格,1个图形和模型预测,分别如下说明。
编号 名称 说明 1 模型初始参数 初始值参数表格,即输入的参数传下 2 模型参数估计值 各个参数的估计值,显著性检验及置信区间等,用于判断参数的显著性情况及模型拟合效果情况等 3 模型拟合效果 模型R 方值,MSE 值等,用于判断模型拟合效果情况 4 模型拟合图 直观展示模型拟合情况,用于判断模型拟合效果情况,如果X个数大于1时无此图 5 模型预测 输入X数据,展示出模型预测y值 -
5、文字分析
模型初始参数 参数 初始值 下界 上界 b1 14 - - b2 -0.79 - - b3 -0.042 - - 上表格展示输入的模型初始参数值,如果没有设置过初始值,默认初始值为1。
模型参数估计值(n =39) 参数项 回归系数 标准误 t 值 p 值 95% CI b1 14.804 0.081 182.489 0.000 14.640 ~ 14.969 b2 -0.579 0.012 -46.577 0.000 -0.604 ~ -0.554 b3 -0.054 0.001 -38.752 0.000 -0.056 ~ -0.051 上表格展示出3个参数的估计值,如果涉及模型中各参数的专业意义,比如本案例中参数b1代表当前拟合模型的渐近线值,否则无其它特殊的意义,其目的仅为了得到数学上的估计模型表达式,用于进一步预测使用等。如果说p 值小于0.05则说明参数具有统计学意义(也或者95%置信区间不包括数字0),如果各个参数均具有统计学意义,一般也可从侧面说明模型拟合效果较好。
模型拟合效果 差异源 平方和SS df 均方MS F p 值 回归 5744.827 3 1914.942 746977.45 0.000 残差 0.092 36 0.003 未校正总计 5744.92 39 校正总计 64.411 38 模型R 方:0.999 
上表格展示出模型拟合情况,通常可查看R 方来判断模型拟合效果,本案例时R 方值接近于1,意味着本次的logistic模型非常有效的拟合了我国人口增长数据(1978~2016),至于F 检验,在非线性回归模型时使用较少,通常不使用此指标。接着使用拟合图直观展示拟合效果如下图:
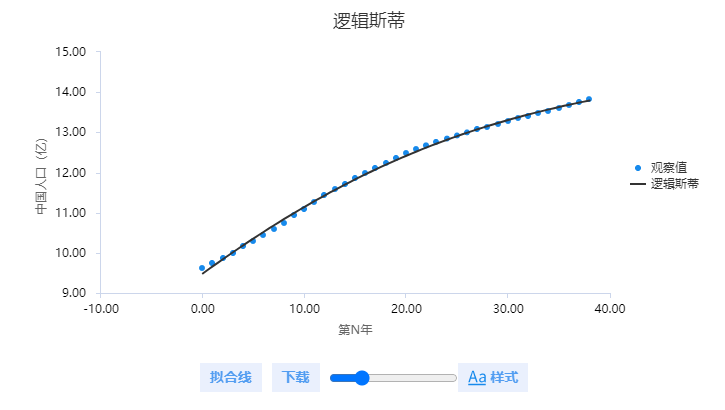
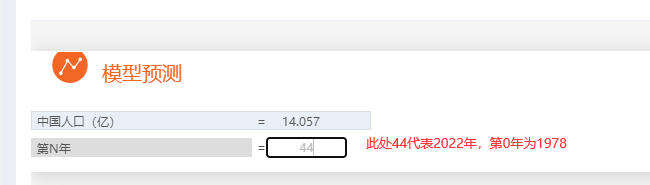
上图直观展示本次人口增长logistic模型拟合效果情况。从图中也可看出,实际数据与拟合数据基本完全吻合在一起,说明拟合效果非常好。因而当前模型可使用,因此用于预测2022年的数据,自变量x为第N年,2022年为第44年,因此输入数字44,得到2022年的人口数据为14.057亿。
-
6、剖析
-
特别提示:
-
关于初始值。初始值是由研究人员输入的一个‘大概’值,即参数的大概估计值,大概预期的值,与此同时,也可设置参数的范围,即上下界,但通常情况下不设置上下界值,除非认为有必要,通常不需要设置上下界值。
-
关于初始值的设置方法。通常包括两种,一是结合专业知识进行判断,二是利用模型公式时的特殊点(比如X=0时,Y=?)去求解得到。专业知识判断上,某参数的实际意义为数据的最大值,那么就设定该参数为最大值即可。SPSSAU默认以数字1作为参数值。
-
参数估计值的95%置信区间使用t 检验进行估计。
-
