多元方差分析MANOVA
-
案例数据下载 下载
-
方差分析是研究X对于Y的差异关系,此处X是定类数据,Y是定量数据。当X的个数或者Y的个数超过一个时,其又可具体进行细分,如下表格所述。
X个数 Y个数 分析方法名称 SPSSAU位置 1 1 单因素方差 通用方法-》方差 多个 1 多因素方差 进阶方法-》双因素方差/三因素方差/多因素方差 1个或多个 多个 多元方差MANOVA 进阶方法-》多元方差MANOVA 如果X仅1个且Y仅1个,此时称作单因素方差分析,此种情况的使用频率最高,绝大多数分析均是此种单因素方差分析,在SPSSAU通用方法的‘方差’按钮即可实现,并且SPSSAU可让放入多个X,循环进行单因素方差分析。如果X的个数大于1个并且Y仅1个时,此时可统称为多因素方差,即X的个数大于1个,具体细分上出于X的具体个数又可称作双因素/三因素等,甚至四因素方差(即X为4个Y为1个)。如果Y的个数大于1个(此时不论X个数1个或多个),均称作多元方差(多因变量方差,multivariate analysis of variance,简称MANOVA)。与此同时,在方差分析如果还有协变量,那么也称作协方差分析(此称呼是为了强调有协变量而已)。
绝大多数情况下,我们都会使用单因素方差(其默认就称作方差分析),其具有较强的稳健性能,检测结果容易接受。但在相关实验数据情况下,则会使用到多因素方差或者多元方差MANOVA,事实上多元MANOVA的Y为多个,其有点类似于重复性多个Y进行方差,但其考虑多个Y间的关系,即考虑到SSCP矩阵(平方和与叉积矩阵,其用于衡量Y自身波动以及Y之间协作波动情况),因而当有多个Y时,可考虑使用多元方差分析MANVOA。具体是否应该使用多元方差分析MANOVA,建议以文献依据,或者对比着不同方法进行决择。
多元方差分析MANOVA案例
-
1、背景
当前有一份医学研究数据共1481条,包括两个Y和两个X(具体X或Y的意义此处不进行说明),数据如下:
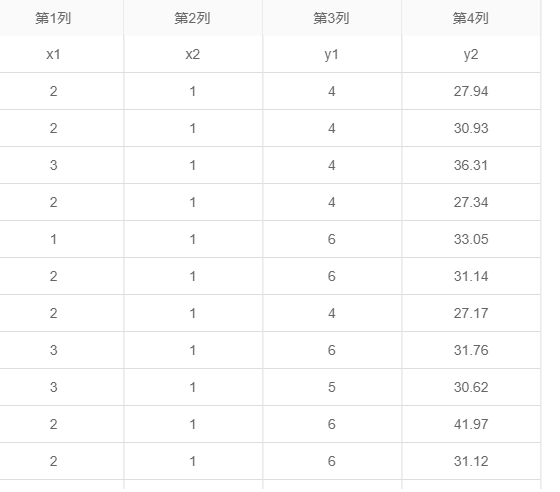
2个X均为定类数据,两个Y均为定量数据,本案例暂没有协变量数据。
-
2、理论
-
多元方差分析MANOVA时,通常情况下其需要满足几项假定条件,分别如下所述:
-
因变量Y需要满足正态性;
-
样本数据之间相互独立;
-
组间方差协方差矩阵相等,即方差齐性。
上述3条要求时,第1条因变量Y需要满足正态性,如果研究数据较多比如大于30(大样本的划分标准),通常可忽略该假定条件,SPSSAU默认提供“Shapiro-Wilk多元正态性检验”。样本数据之间不能有关联性,比如第1行数据影响到第2行数据等。数据还需要满足方差齐性,即进行方差齐检验,方差分析具有较强的稳健性,很多时候即使不满足方差齐性,也可得到科学结论,因而有时候并不关注此前提条件。SPSSAU默认提供“协方差矩阵Box方差齐性检验”结果。
需要提示的是:样本数据之间相互独立较容易满足。但是因变量Y满足正态性,以及方差齐性这两个条件,很多时候并不容易满足,实际分析研究时,如果是实验式数据,其数据相关规整且偏离两个条件(正态和方差齐性)的幅度不大,因而通常可‘容忍式接受’即直接使用MANOVA。但如果是非实验式数据比如问卷研究数据,此种情况不建议使用MANOVA,因为此类数据时容易出现某个X的类别样本很多或者很少,即X的类别极其不均匀,并且因变量Y并不是完全的连续式数据,因而导致数据极其不满足正态或者方差齐性,严重违反前提条件因而得出的结论不科学。
-
-
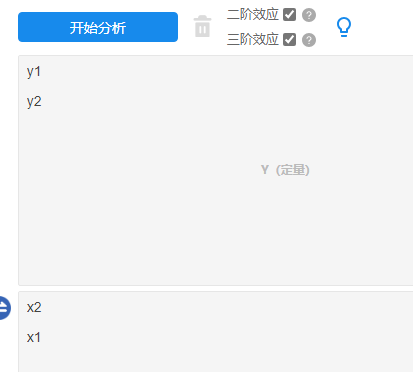
3、操作
本例子中操作截图如下,默认选中二阶效应和三阶效应,二阶效应是指任意两个X之间的交互效应,三阶效应指任意3个X之间的交互效应(需要注意的是,SPSSAU提供的多元方差MANVOA分析时最多支持3个X)。
-
4、SPSSAU输出结果
多元方差分析MANOVA一共输出4个表格,说明如下:
表格名称 说明 多变量检验结果 展示多变量检验结果,查看组间差异信息等 单变量检验结果 展示某个因变量Y时对应的检验结果,循环输出 协方差矩阵Box方差齐性检验 展示方差齐性检验结果 Shapiro-Wilk多元正态性检验 展示正态性检验结果 -
5、文字分析
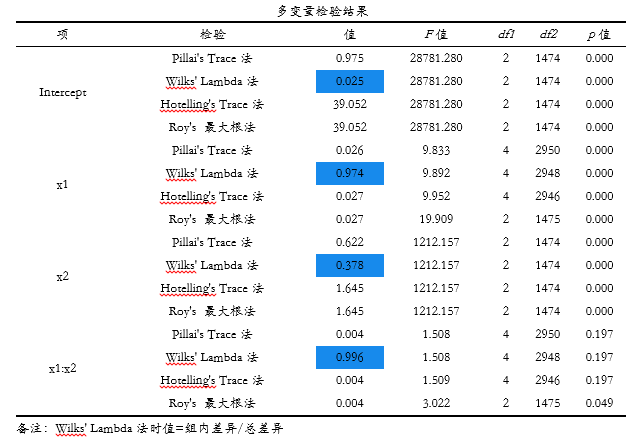
多变量检验结果表格,其展示四种检验,分别是Pillai's Trace法、Wilks' Lambda法、Hotelling's Trace法和Roy's 最大根法,四种检验的功能一致,其均用于检验组间是否存在着差异性,但具体使用哪一种检验结果并无固定式标准。通常情况下,建议查阅“Wilks' Lambda法”,因为其对应的‘值’,其意义为组内差异除以总差异,比如上表格中X1为0.974,共意义为组内差异为97.4%,组间差异则为2.6%,一般关注的是组间差异,因而希望Wilks' Lambda值越小越好。但另外3种检验时的‘值’并无此特点。另外,相对来看,使用Pillai's Trace法进行差异显著性查看的情况相对较多。
通过最后四列分别是F 值,两个自由度值和p 值,如果对应的p 值小于0.05,那么说明该项(比如上表格中的X1、X2或者交互项X1:X2)的组间差异是否具有显著性,即整体上看某项对于整体Y是否具有差异性。上表格可以看到,如果使用Pillai's Trace法结果,那么X1和X2均呈现出显著性,即具有显著的组间差异,并且4个检验的结论均具有一致性,即更加可靠的结论为X1和X2均对于Y具有显著性差异,但是X1与X2的交互项显示不具有显著性(3个检验时的p 值>0.05,仅Roy's 最大根法的p 值=0.049<0.05),此种情况一般以交互项不具有显著性作为结论。
多变量检验结果是针对X对于所有Y的差异检验,那么接着还需要查看X对于具体每个Y的差异,因而可查阅接下来的单变量检验结果表格(如果从分析上,也可直接使用SPSSAU进阶方法里面的多因素方差分析进行研究)。
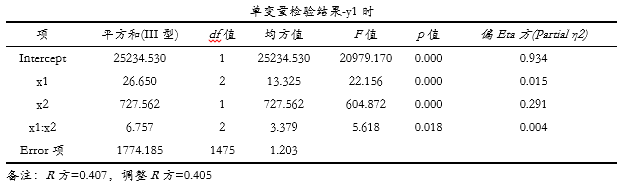
上表格展示y1时的检验结果,显示x1呈现出显著性,但是x2并没有呈现出显著性,交互项呈现出显著性。这与多变量检验结果不一致,多变量检验结果显示x1或x2均有显著性但交互项不具有显著性,此种情况较为正常。在分析流程上,如果是使用多元方差MANOVA,意味着将Y作为整体考虑,因而首先需要满足多变量检验,然后再看具体每个Y时即单变量检验结果,在多变量检验结果时显示交互项不具有显著性,分析上可直接不考虑接下来单变量检验结果的交互项,即使其呈现出显著性。与此同时上表格还展示出效应量结果偏Eta方值,以研究值实际需要进行取舍使用即可。
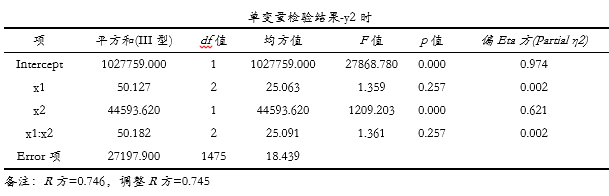
类似地,可查阅y2时的单变量检验结果,其显示x1呈现出显著性,但是x2并没有呈现出显著性,交互项呈现出显著性。这与多变量检验结果不一致,多变量检验结果显示x1或x2均有显著性但交互项不具有显著性。

上表格展示方差齐检验结果,Box’s M检验的原假设是具有方差齐性,如果p 值>0.05则意味着数据具有方差齐性,反之意味着数据不具有方差齐性。本案例结果显示数据不具有方差齐性,但正如上述所述,多元方差MANOVA分析具有较强稳健性,因而本处也依旧使用上述结果。

上表格展示正态性检验结果,Shapiro-Wilk检验的原假设是具有正态性,如果p 值>0.05则意味着数据具有正态性,反之意味着数据不具有正态性。上表格显示整体上数据不具有正态性。当然研究者可分别针对每个Y进行正态性检验等均可,本案例数据有1481条且为连续数据,因而不考虑正态性这一前提假定条件。
-
6、剖析
多元方差分析MANOVA分析涉及以下几个关键点,分别如下:
-
多元方差分析MANOVA时,如果希望进行事后多重比较?
-
此时应该使用SPSSAU进阶方法里面的具体方法,分别重复进行,比如2个X时使用双因素方差分析。
-
多元方差分析MANOVA时,希望进行简单效应分析?
-
此时应该使用SPSSAU进阶方法里面的具体方法,分别重复进行,比如2个X时使用双因素方差分析。
-
多变量检验结果与单变量检验结果不一致?
-
多变量检验结果是针对所有因变量Y的差异检验,并且其考虑变量Y间的协同变化差异,因而二者结果不一致是正常现象。
-
多变量检验结果的四种检验应该使用哪一种?
-
多变量检验共提供四种检验,具体使用哪一种并没有固定标准。一般使用Wilks' Lambda法查看组间差异。相对来看,使用Pillai's Trace法进行差异显著性查看的情况相对较多。
-