-
判别分析(distinguish analysis)是一种机器学习算法,其用于在分类确定前提下,根据数据的特征研究数据归类问题。比如结合消费者的特征数据(比如消费金额、消费频次、购物时长、购买产品种类等),以预测消费者属于某种类型的顾客(款式偏好型、质量在乎型、价格敏感型等)。
判别分析时,通常需要将数据分为两部分。一部分是训练模型数据,一部分是验证模型数据。训练模型数据是指比如有200个消费者,并且知道此200个消费者的类别情况;判别分析利用此200个消费者的特征及类别,训练拟合出一个模型。那么此模型是好还是坏呢? 接着再利用另一部分验证模型数据进行验证。判别分析拟合出的训练模型,如果在测试集数据上,也表现良好,那么说明拟合模型非常好。后面可以利用此模型用于预测其它“没有类别”只有特征的数据,用于预测得到新顾客的类别情况,最终产生商业价值。
一般情况下,训练集和测试集的比例是9:1,即使用90%的数据用于训练拟合模型,余下10%的数据用来验证模型;切记最终模型质量好或坏,一般情况下以验证模型的预测准确率作为判断标准。利用拟合模型预测测试集的类别,并且与训练集已知类别进行交叉,判断预测准确率,如果预测准确率较高比如大于80%,一般就说明拟合模型良好。
判别分析有多种,比如距离判别,Fisher判别(典型判别,线性判别分析、Fisher线性判别),Bayes判别等。其中Fisher判别使用频率最高,原因在于其对数据特征的分布没有任何限制,SPSSAU默认使用Fisher线性判别(下述全部为线性判别,Linear Discriminant Analysis,LDA)进行分析。
-
特征:即研究项,用来拟合模型的数据项;
-
判别类别:即被预测的类别,特征数据预测类别;
-
训练集:用来拟合模型的数据;
-
测试集(验证集):用于验证模型质量的数据;
特别提示,判别分析中会出现以下术语:
-
线性判别分析案例
-
1、背景
本次数据使用最为经典的鸢尾花卉数据集。此数据是判别分析中经典的案例数据。该数据是利用花萼长、花萼宽、花瓣长、花瓣宽共4个特征,来预测花的种类(共3类:分别是刚毛鸢尾花、变色鸢尾花和佛吉尼亚鸢尾花;下面全部是类别1,类别2和类别3表示)。数据共有150个样本,包括4个特征和一个预测类别。
由于数据较少共150个,预期先将样本分为8:2,即80%共120个样本作为训练模型使用;余下20%即30个样本作为验证模型使用。
-
2、理论
判别分析是一种机器学习算法,其原理在于利用已知信息(已经特征对应着类别)进行拟合训练模型,并且验证模型的质量。如果模型质量高,此时将此模型利用到其它类别的未知类别数据上使用。
-
模型质量的好坏,通常是由测试集数据的预测准确率进行判断(而不是训练集模型);
-
模型质量的判断指标共有3个:分别是预测正确率Precision、召回率Recall和F1-score。正确率是指预测为某类别时,实际情况下属于该类别的样本比例;召回率是指实际为某类别时,被正确预测到该类别的样本比例;F1-score值是指正确率与召回率的加权综合指标,其计算公式为F1-score = 2*正确率*召回率 / (正确率+召回率)。
-
为什么一定需要使用测试集数据的预测情况作为模型质量判断标准呢?原因在于判别分析可能会出现‘过拟合’现象,即在当前数据上拟合的非常好,但跑到别的数据上面就出现预测错误。
特别提示
-
-
3、操作
本例子包括4个特征,并且将训练集和测试集比例按8:2进行,SPSSAU操作如下图:
-
4、SPSSAU 输出结果
SPSSAU共输出4个表格,分别是模型训练集和测试集分布、各分类判别函数、训练集预测准确率和测试集预测准确率。
模型训练集和测试集分布:用于展示训练集和测试集的比例及样本量情况。
各分类判别函数:此为模型的拟合公式(函数),如果后续需要用此模型进行类别预测,可使用判别函数进行计算,如果使用判别分析的目的在于后续进行数据预测,则判别函数非常重要,下述文字分析会详细说明。
训练集预测准确率:拟合出模型后,将模型用于训练数据的预测准确率判断。此表格仅能说明训练数据拟合出的模型,对于训练数据的预测准确率情况,通常训练集预测准确率均很高。但是判别分析可能出现‘过拟合’现象,因此最终需要使用测试集预测准确率进行判断模型质量好坏。
测试集预测准确率:最终用于验证模型的质量好坏。
-
5、文字分析
模型训练集和测试集分布 比例% 样本N 训练集 80% 120 测试集 20% 30 总结 100% 150 本次判别分析(LDA)共针对150个数据进行研究,选择数据中前80.00%即120个数据作为训练集,用于训练拟合判别分析模型;余下20.00%即30个数据作为测试集,用于验证模型有效性。
各分类判别函数 类别1(刚毛鸢尾花) 类别2(变色鸢尾花) 类别3(佛吉尼亚鸢尾花) 截距 -674.591 -573.567 -774.160 花萼长 21.420 18.194 17.001 花萼宽 14.079 2.091 0.653 花瓣长 -12.674 -1.226 2.060 花瓣宽 -10.461 4.804 14.192 上表格展示各类别对应的判别函数(数学关系表达式),当前类别数量为3,每个类别均会对应一个表达式,如下:
-
类别1 = -674.591 + 21.420*花萼长 + 14.079*花萼宽-12.674*花瓣长-10.461*花瓣宽
-
类别2 = -573.567 + 18.194*花萼长 + 2.091*花萼宽-1.226*花瓣长 + 4.804*花瓣宽
-
类别3 = -774.160 + 17.001*花萼长 + 0.653*花萼宽 + 2.060*花瓣长 + 14.192*花瓣宽
-
特别说明
-
预测类别为3个,所以会有3个数学关系表达式(如果类别为4个或更多,则对应有4个或更多数学关系表达式);如果新的数据(只有特征没有类别)想进行预测,如下图所示,下图中有3个数据需要预测,那么分别代入3个公式得到每个判别类别的判别分,对应分值最高的类别,就为最终归属类别。比如第一个预测样本数据,分别是50,33,14和2;
-
代入判别类别1时: -674.591 + 21.420*50 + 14.079*33-12.674*14-10.461*2=662.658;
-
代入判别类别2时:-573.567 + 18.194*50 + 2.091*33-1.226*14 + 4.804*2=397.58;
-
代入判别类别3时: -774.160 + 17.001*50 + 0.653*33 + 2.060*14 + 14.192*2=154.663;
-
662.658属于判别类别1(即刚毛鸢尾花),最终特征数据为50,33,14和2时,应该预测为类别1(即刚毛鸢尾花)。
花萼长 花萼宽 花瓣长 花瓣宽 判别类别1 判别类别2 判别类别3 最终归属类别 50 33 14 2 662.658 397.58 154.663 类别1 67 31 56 24 236.19 756.892 841.118 类别3 89 31 51 23 781.261 1158.486 1190.648 类别3 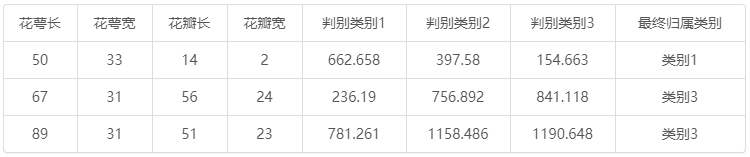
-
如果预测类别为1个,此类数据无意义;永远都会预测为一个类别;
-
如果预测类别为2个,此时仅会提供1个判别函数,利用该判别函数代入计算,如果得出的判别值大于0,则属于类别2;如果得出的判别值小于0,则属于类别1。
训练集预测准确率 预测类别 样本量N 正确率Precision 召回率Recall F1-score 类别1(刚毛鸢尾花) 40 100.00% 100.00% 100.00% 类别2(变色鸢尾花) 40 97.37% 92.50% 94.87% 类别3(佛吉尼亚鸢尾花) 40 92.86% 97.50% 95.12% 汇总 120 96.74% 96.67% 96.70% 上表格展示训练集即120个样本数据的预测准确率;上表显示整体正确率为96.74%,并且各个类别的正确率均高于90%。除此之外,整体召回率为96.67%,3个类别对应的召回率均高于90%。除此之外,F1-score值也均高于90%。整体上训练集数据的模型拟合非常好。
-
训练集数据预测准确率情况仅作简要参考,最终应该以测试集预测准确率
特别提示
测试集预测准确率 预测类别 样本量N 正确率Precision 召回率Recall F1-score 类别1(刚毛鸢尾花) 10 100.00% 100.00% 100.00% 类别2(变色鸢尾花) 10 100.00% 100.00% 100.00% 类别3(佛吉尼亚鸢尾花) 10 100.00% 100.00% 100.00% 汇总 30 100.00% 100.00% 100.00% 上表展示测试集即30个样本数据的预测准确率;上表显示整体正确率为100%,并且各个类别的正确率均为100%。除此之外,整体召回率和3个类别对应的召回率均为100%。也即说明测试集显示数据全部预测准确,没有预测出错的现象。模型拟合质量非常高。
6、剖析
涉及以下几个关键点,分别如下:
-
如果预测类别中出现小数,则会提示“分类数据必须为整数”。
-
预测集中的类别与测试集中的类别不一致,则会提示“训练数据中出现未知类别”。
-
如果预测类别为1个,此类数据无意义;永远都会预测为一个类别。
-
如果预测类别为2个,此时仅会提供1个判别函数,利用该判别函数代入计算,如果得出的判别值大于0,则属于类别2;如果得出的判别值小于0,则属于类别1。
-
预测类别为3个,所以会有3个数学关系表达式(如果类别为4个或更多,则对应有4个或更多数学关系表达式);如果新的数据(只有特征没有类别)想进行预测,如下图所示,下图中有3个数据需要预测,那么分别代入3个公式得到每个判别类别的判别分,对应分值最高的类别,就为最终归属类别。
-
多数情况下判别分析用于预测数据,但有时候可使用判别分析用于辅助判断聚类分析的效果情况。
-
