-
聚类分析是通过数据建模简化数据的一种方法,“物以类聚,人以群分”正是对聚类分析最好的诠释。从分析角度上看,聚类分析可分为两种,一种是按样本(或个案)聚类,此类聚类的代表是K-means聚类方法;另外一种是按变量(或标题)聚类,此类聚类的代表是分层聚类。具体聚类方式的概括如下表:
-
聚类方式 数据类型 聚类算法名称 按样本(个案) 定量 K-means聚类 按样本(个案) 定量和定类,或仅定类 K-prototype聚类 按变量(标题) 定量 分层聚类 如果是按样本聚类,则使用SPSSAU的进阶方法模块中的“聚类分析”功能,其会自动识别出应该使用K-means聚类算法还是K-prototype聚类算法。
如果是按变量(标题)聚类,此时应该使用分层聚类,并且结合聚类树状图进行综合判定分析,得出科学分析结果。比如当前有8个裁判对于300个选手进行打分,试图想对8个裁判进行聚类,以挖掘出裁判的打分偏好风格类别情况。此时则需要进行分层聚类。
-
分层聚类有几点需要特别注意:
-
1:仅针对定量数据进行分层聚类;
-
2:如果数据的单位有较大差别,可首先对于数据进行标准化处理后,针对标准化数据进行分层聚类;
-
3:由于均为定量数据,因而从原理角度上,分层聚类时应该使用Pearson相关系数去度量距离,相关系数值越大说明越紧密,则说明距离越近,相关系数值越小说明越疏远,说明距离越远;SPSSAU默认使用Pearson相关系数表示距离大小;
-
4:SPSSAU进行分层聚类时使用组平均距离法进行聚类;通俗地讲即首先将相关性最强的两项聚成一类(第一个合并簇),接着找出与该“合并簇”相关性最强的第三项,聚类成第二个合并簇,接着为第三个合并簇,依次循环迭代此过程,直至结束。
-
-
分层聚类案例
-
1、背景
当前有8个裁判对300名选手打分,最低分为1分,最高分为10分;希望对8个裁判进行聚类,以识别出裁判的风格类型。总共8个裁判共有8列数据,并且共有300行。由于打分全部均是从1到10分,8列数据的单位均一样,因此在分析之前不需要进行标准化数据(当然进行标准化处理也没有问题)。
-
2、理论
聚类分析是“物以类聚,人以群分”的研究方法,从分析角度上看,聚类分析可分为两种,一种是按样本(或个案)聚类,此类聚类的代表是K-means聚类方法;另外一种是按变量(或标题)聚类,此类聚类的代表是分层聚类。具体聚类方式的概括如下表:
聚类方式 数据类型 聚类算法名称 按样本(个案) 定量 K-means聚类 按样本(个案) 定量和定类,或仅定类 K-prototype聚类 按变量(标题) 定量 分层聚类 针对分层聚类,涉及理论或注意项如下:
-
1:仅针对定量数据进行分层聚类;
-
2:如果数据的单位有较大差别,可首先对于数据进行标准化处理后,针对标准化数据进行分层聚类;
-
3:由于均为定量数据,因而从原理角度上,分层聚类时应该使用Pearson相关系数去度量距离,相关系数值越大说明越紧密,则说明距离越近,相关系数值越小说明越疏远,说明距离越远;SPSSAU默认使用Pearson相关系数表示距离大小;
-
4:SPSSAU进行分层聚类时使用组平均距离法进行聚类;通俗地讲即首先将相关性最强的两项聚成一类(第一个合并簇),接着找出与该“合并簇”相关性最强的第三项,聚类成第二个合并簇,接着为第三个合并簇,依次循环迭代此过程,直至结束。
-
-
3、操作
本案例中总共涉及8个标题,SPSSAU操作截图如下:
SPSSAU会默认聚类为3类并且呈现表格结果,如果希望更多的类别个数,可自行进行设置。
-
4、SPSSAU输出结果
SPSSAU会首先输出聚类项的基本描述情况,接着输出每项的聚类类别归属情况;并且输出树状图,如下所述:
聚类项描述分析 名称 样本量 最小值 最大值 平均值 标准差 中位数 裁判1 300 7.000 10.000 8.496 0.867 8.500 裁判2 300 7.100 10.000 8.918 0.820 9.000 裁判3 300 7.000 9.800 8.085 0.817 8.000 裁判4 300 7.200 9.900 8.970 0.677 9.100 裁判5 300 7.000 9.500 8.038 0.674 7.900 裁判6 300 7.000 10.000 8.876 0.959 9.100 裁判7 300 7.000 10.000 8.181 0.979 8.000 裁判8 300 7.000 10.000 8.470 1.038 8.400 上表格展示总共8个分析项(即8个裁判数据)的基本情况,包括均值,最大或者最小值,中位数等,以便对于基础数据有个概括性了解。整体上看,8个裁判的打分基本平均在8分以上。
-
特别提示
-
上表格中的值与聚类的原理基本没有关联性,请勿将上表格信息与聚类结果产生联系
聚类类别分布表 名称 所属类别 裁判8 Cluster_1 裁判5 Cluster_2 裁判3 Cluster_2 裁判7 Cluster_2 裁判1 Cluster_3 裁判6 Cluster_3 裁判2 Cluster_3 裁判4 Cluster_3 总共聚类为3个类别,以及具体分析项的对应关系情况。在上表格中展示出来,上表格可以看出:裁判8单独作为一类;裁判5,3,7这三个聚为一类;以及裁判1,6,2,4作为一类。
聚类类别与分析项上的对应关系可以在上表格中得到,同时也可以查看聚类树状图得出更多信息。至于聚类类别分别应该叫做什么名字,这个需要结合对应有关系情况,自己单独进行命名。
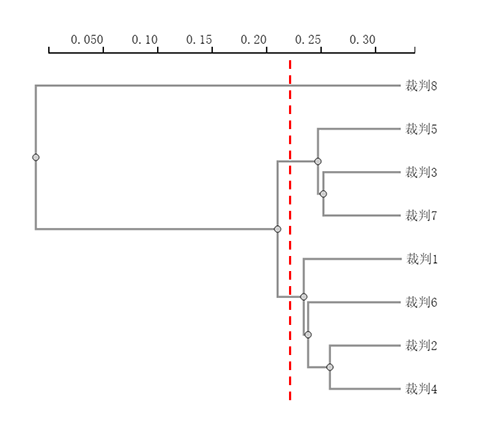
上图为聚类树状图的展示,聚类树状图是将聚类的具体过程用图示法手法进行展示;最上面一行的数字仅仅是一个刻度单位,代表相对距离大小;一个结点表示一次聚焦过程。
树状图的解读上,建议单独画一条垂直线,然后对应查看分成几个类别,以及每个类别与分析项的对应关系。比如上图中,红色垂直线最终会拆分成3个类别;第1个类别对应裁判8;第2个类别对应裁判5,3,7;第3个类别对应裁判1,6,2,4。
当然在分析时也可以考虑分成2个类别,此时只需要对应将垂直线移动即可,如下图:
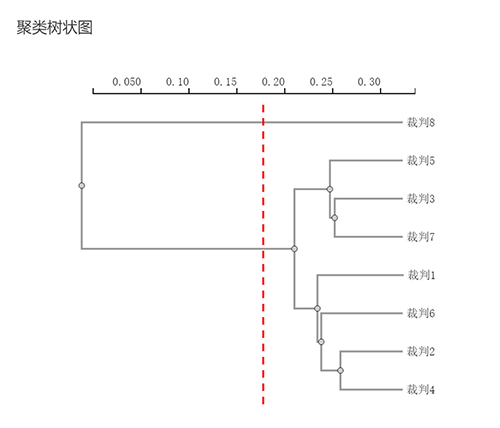
上图展示出仅分为2个类别时的情况;如果聚类成2个类别;此时裁判8单独作为一个类别;裁判5,4,7,1,6,2,4会单独聚为一类。
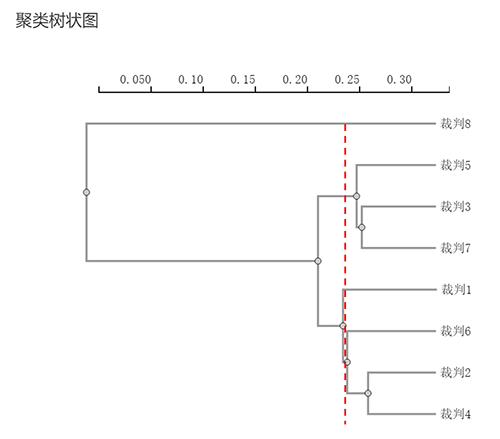
如果是聚为四类;从上图可看出,明显的已经不再合适。原因在于垂直线不好区分成四类。也即说明有2个类别本应该在一起更合适(上图中的裁判1与6/2/4);但是如果分成4类,此时裁判1会单独成一类。所以画垂直线无法区分出类别。
因而综合分析来看,最终聚类为3个类别最为适合。
-
-
5、文字分析
具体文字分析例子如下:
本次研究共涉及8个裁判对于300个选手的打分数据,打分从1到10分;并没有量纲问题,因而对平数据不需要进行标准化处理(特别提示:如果有量纲单位问题,最好先进行标准化处理)。使用SPSSAU 13.0版本软件进行研究;具体分层聚类时使用Pearson相关系数度量距离大小,同时使用组平均距离法进行分析。
结合聚类树状图进行分析,如果聚类为一个类别,此时其中一个类别仅对应1项,另外一个类别对应7项;如果聚类为四个类别,其中有一项无法很好的区分成一类;最终聚类为三类最为合适,第1个类别对应裁判8;第2个类别对应裁判5,3,7;第3个类别对应裁判1,6,2,4。
-
6、剖析
针对分层聚类,需要注意以下几点:
-
1:针对定量数据进行分析;
-
2:如果数据量纲不同(即单位不一致),分析前一般需要对所有分析项进行标准化处理(SPSSAU的生成变量->标准化功能);
-
3:分层聚类使用Pearson系数度量距离大小,以及使用组平均距离法进行聚类;
-
4:分层聚类出来,具体聚成几个类别较好,建议结合聚类树状图和实际数据情况进行分析对比。
-
