协方差分析

  • 当X为定类数据，Y为定量数据时，通常使用的是方差分析进行差异研究。比如性别对于身高的差异。

      • X的个数为一个时，称之为单因素方差（很多时候也称方差分析）；

      • X为2个时则为双因素方差；

      • X为3个时则称作三因素方差，依次下去。

      • 当X超过1个时，统称为多因素方差，很多时候也统称为方差分析。

    • 如果在方差分析过程中，会有干扰因素；比如“减肥方式”对于“减肥效果”的影响，年龄很可能是影响因素；同样的减肥方式，但不同年龄的群体，减肥效果却不一样；年龄就属于干扰项，因此在分析的时候需要把它纳入到考虑范畴中。如果方差分析时需要考虑干扰项，此时就称之为协方差分析，而干扰项也称着“协变量”。

      通常情况下，协变量是定量数据，比如本例中的年龄，协变量的个数不定，但一般情况下会很少，比如为1个，2个；原因在于协变量并非核心研究项，只是可能干扰到模型所以放到模型中；如果放入过多的协变量，反而会出现‘主次不分’，因此在进行协方差分析时，需要相对谨慎的放入干扰项（即协变量）。

      在实验研究中，比如研究者测试某新药对于胆固醇水平是否有疗效；研究者共招募72名被试，分为A和B共两组，每组分别是36名，A组使用新药，B组使用普通药物；在实验前先测试72名被试的胆固醇水平，以及在实验3月之后再次测定胆固醇水平。

      为测试新药是否有帮助，因此使用方差分析对比两组被试在3月后胆固醇水平的差异性；如果有差异具体差异是什么，通过差异去研究新药是否有帮助；在这里出现一个干扰项即实验前的胆固醇水平（实验前胆固醇水平肯定会影响实验后的胆固醇水平），因此需要将实验前的胆固醇水平纳入模型中，因此此处需要进行协方差分析。

      • 特别提示:

      • 对于协方差分析，X是定类数据，Y是定量数据；协变量为定量数据；如果协变量是定类数据，可考虑将其纳入X即自变量中，也或者将协变量作虚拟变量处理；

      • 协变量为干扰项，但并非核心研究项；因此通常情况下只需要将其纳入模型中即可，并不需要过多的分析；

      • 协方差分析有一个重要的假设即“平行性检验”，如果交互项（即有*号项）的p 值>0.05则说明平行，满足“平行性检验”，可进行分析。

      • 如果协方差分析不满足“平行性”，交互项（即有*号项）的p 值< 0.05则说明不平行，不满足“平行性检验”，此时则应该将协变量项移出。

      • “平行性”是指：自变量X与协变量对于因变量Y的影响时，自变量X与协变量之间保持独立性。

      SPSSAU分析结果表格示例如下

      协方差分析结果
      差异源 平方和 df 均方 F p
      Intercept 1.430 1 1.430 6.077 0.016*
      药物 0.058 1 0.058 0.246 0.621
      胆固醇水平实验前 0.001 1 0.001 0.003 0.954
      药物*胆固醇水平实验前 0.037 1 0.037 0.156 0.694
      Residual 15.997 68 0.235 null null
      R 2 : 0.083
      * p <0.05 ** p <0.01
      • 特别提示：

      • 上表格中“药物*胆固醇水平实验前”即为平行检验项，其对应的p 值为0.694>0.05,即说明通过平行性检验，可以进行协方差分析。因而最终进行协方差分析时，应该把“平行性检验”这个选项去掉，此项的目的只是为了检验平行性，而不是最终的协方差分析。

  • 协方差分析

    • 1、背景

      某研究者测试新药对于胆固醇水平是否有疗效；研究者共招募72名被试，分为A和B共两组，每组分别是36名，A组使用新药，B组使用普通药物；在实验前先测试72名被试的胆固醇水平，以及在实验3月之后再次测定胆固醇水平。

      为测试新药是否有帮助，因此使用方差分析对比两组被试在3月后胆固醇水平的差异性；如果有差异具体差异是什么，通过差异去研究新药是否有帮助；在这里出现一个干扰项即实验前的胆固醇水平（实验前胆固醇水平肯定会影响实验后的胆固醇水平），因此需要将实验前的胆固醇水平纳入模型中，因此此处需要进行协方差分析。

    • 2、理论

      协方差分析，其实质还是方差分析，但多出干扰项即协变量时，此时则称之为协方差分析。

      • 特别提示:

      • 对于协方差分析，X是定类数据，Y是定量数据；协变量为定量数据；如果协变量是定类数据，可考虑将其纳入X即自变量中，也或者将协变量作虚拟变量处理；

      • 协变量为干扰项，但并非核心研究项；因此通常情况下只需要将其纳入模型中即可，并不需要过多的分析；

      • 协方差分析有一个重要的假设即“平行性检验”，如果交互项（即有*号项）的p 值>0.05则说明平行，满足“平行性检验”，可进行分析。

      • 如果协方差分析不满足“平行性”，交互项（即有*号项）的p 值< 0.05则说明不平行，不满足“平行性检验”，此时则应该将协变量项移出。

      • “平行性”是指：自变量X与协变量对于因变量Y的影响时，自变量X与协变量之间保持独立性。

    • 3、操作

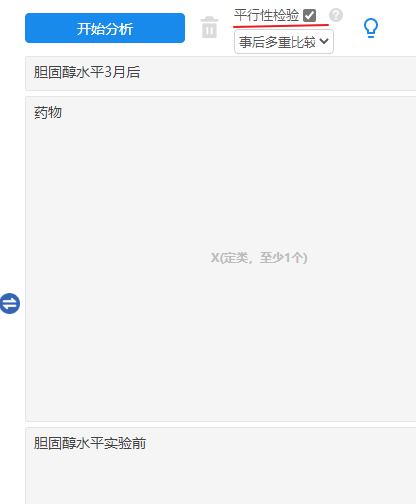
      本例子中研究1个X对于Y的差异，并且有协变量；X为药物， Y为“胆固醇水平3月后”，协变量为“胆固醇水平实验前”，SPSSAU放置如下：

      • 如果需要进行平行性检验，“平行性检验”框需要打勾；

      • 如果满足平行性检验后进行最终协方差分析，“平行性检验”框不能打勾。

    • 4、SPSSAU输出结果

      协方差分析结果
      差异源 平方和 df 均方 F p
      Intercept 1.430 1 1.430 6.077 0.016*
      药物 0.058 1 0.058 0.246 0.621
      胆固醇水平实验前 0.001 1 0.001 0.003 0.954
      药物*胆固醇水平实验前 0.037 1 0.037 0.156 0.694
      Residual 15.997 68 0.235 null null
      R2 : 0.083
      * p <0.05 ** p <0.01

      上表为平行性检验结果，表中“药物*胆固醇水平实验前”此项为自变量X与协变量的交互项，通过对交互项分析可知，数据通过平行性检验(F =0.003,p =0.954>0.05）,因而说明数据适合进行协方差分析。因而最终进行协方差分析，并且结果如下表所示：

      协方差分析结果
      差异源 平方和 df 均方 F p
      Intercept 2.812 1 2.812 12.099 0.001**
      药物 1.405 1 1.405 6.045 0.016*
      胆固醇水平实验前 0.001 1 0.001 0.003 0.954
      Residual 16.033 69 0.232 null null
      R 2 : 0.081
      * p <0.05 ** p <0.01
      • 特别提示：

      • 第一次需要进行平行性检验(平行性检验”打勾)，如果通过平行性检验，则才能进行协方差分析（平行性检验”框不能打勾），因而两个表格结果不一样，第一个表格是平行性检验的结果；第二个表格是最终结果表格。

    • 5、文字分析

      协方差分析结果
      差异源 平方和 df 均方 F p
      Intercept 2.812 1 2.812 12.099 0.001**
      药物 1.405 1 1.405 6.045 0.016*
      胆固醇水平实验前 0.001 1 0.001 0.003 0.954
      Residual 16.033 69 0.232 null null
      R 2 : 0.081
      * p <0.05 ** p <0.01

      本次数据研究新药对于胆固醇水平的帮助，实验分为AB两组，A组使用新药，B组使用普通药物。并且将实验前的胆固醇水平作为协变量纳入模型中，首先进行平行性检验，平行性检验显示交互项“药物*胆固醇水平实验前”并未来呈现出显著性(F =0.003,p =0.954>0.05）,说明数据通过平行性检验，因而满足协方差分析前提假设。

      上表为协方差分析结果，上表中R 2值为0.081，意味着药物解释胆固醇水平的8.1%变异。研究重点在于药物对于胆固醇水平的帮助，在这里药物呈现出0.05水平的显著性(F =6.045,p =0.016 <0.05），意味着普通药物和新药的两组群体在胆固醇水平上有着显著性差异。具体从下表可知，新药使用B组群体整体胆固醇水平均值为4.991，小于普通药物组别的5.267，即说明新药对于胆固醇水平的帮助性明显更好。

      均值对比
      项 平均值 标准差 N
      普通药物 5.267 0.525 36
      新药 4.991 0.429 36

    • 6、剖析

      • 特别提示:

      • 协方差分析的步骤为：先进行平行性检验(平行性检验”框打勾)；通过平行性检验后，再进行协方差分析(平行性检验”框不能打勾)。如果是进行平行性检验，则此时只看交互项的显著性，其余指标不用理会，包括自变量的显著性情况。

疑难解惑

  • 均方平方和类型？

  • 当前计算均方平方和，算法处理上SPSSAU默认为III型平方和。

  • 事后多重比较与‘单独进行事后多重比较’结果不一致？

  • 单独进行事后多重比较（进阶方法->事后多重比较法）时，模型实质上为单因素方差，仅考虑1个X的情况，标准误差的计算并不一致，因此结果会不一致，但通常情况下结论会保持一致；以及此处事后多重比较使用的是边际估计均值（偏最小二乘均值）与一般意义上的平均值有所区别，类似于SPSS软件的EMMEANS功能。

  • 边际估计均值EMMEANS是什么？

  • 在进行事后多重比较时计算的‘均值差值’是基于‘边际估计均值’进行计算，实验研究中，如果为平衡数据，则‘边际估计均值’与平均值完全一样，如果为非平衡数据，‘边际估计均值’为平均值的‘矫正’，其更为科学和准确；通常来看，‘边际估计均值’和平均值应该非常接近，因为它们的测量意义完全一致。

  • 关于方差分析时的效应量?

  • 如果选中‘效应量’，则SPSSAU会在方差检验表格中输出偏Eta方(Partial η2)，偏Eta方表示效应量大小时，通常情况下效应量小、中、大的区分临界点分别是:0.01，0.06和0.14。与此同时，事后多重表格中会提供cohen d 这一效应量值，通常情况下Cohen's d 值表示效应量大小时，效应量小、中、大的区分临界点分别是:0.20，0.50和0.80。