典型相关分析

•  分析方法视频解读：B站优酷

• 案例数据下载 下载

• 如果研究1个X和1个Y之间的关系情况，此时直接使用相关分析即可；但如果希望研究1组X和1组Y之间的关系情况，则需要使用典型相关分析（canonical correlation analysis，简称caa）。比如投资性变量（如劳动者人数、货物周转量、生产建设投资等）与国民收入变量（如工农业国内收入、运输业国内收入、建筑业国内收入等）这两组数据之间的相关关系；也或者运动员体力指标（如反复横向跳、纵跳、背力、握力等）与运动能力指标（如耐力跑、跳远、投球等）这两组数据之间的相关有关系，此时均需要使用典型相关分析。

  典型相关分析用于研究一组X与另一组Y数据之间的相关关系情况。它借助主成分分析思想，结合变量间的相关关系情况，寻找出一个或少数几个综合变量（即典型变量）来替代原变量，从而对两组变量关系集中到少数几对典型变量间的关系之上。

  • 从步骤上讲：典型相关分析共分为三个步骤。

  • 第一步：提取出典型相关变量【非常重要】；

  • 第二步：寻找典型变量与研究变量之间的关系表达式，以及典型变量与研究变量间的关系情况；

  • 第三步：典型冗余分析。

  • SPSSAU共输出4个表格；表格1用于典型变量表述典型变量之间的相关关系情况；表格2和表格3用于展示典型变量与研究变量间的数学表达式关系和相关有关系；表格4可用于典型冗余分析。

    SPSSAU输出表格参考格式如下【典型相关较为复杂，建议查看案例】:

    
    
    
    
    

• 1、背景

  为研究运动员体力和运动能力之间的相关关系情况。共收集38个学生样本进行分析。测试数据包括体力指标共7项（X1为反复横向跳，X2为纵跳，X3为背力，X4为握力，X5为台阶试验指数，X6为立定体前屈，X7为俯卧向体后仰）；运动能力指标共5项（Y1为50米跑时间，Y2为跳远，Y3为投球，Y4为引体向上，Y5为耐力跑）。

  从上述背景来看，X共由7项表示，Y由5项表示。想研究X和Y这两组指标之间的相关关系情况，不能通过常规的相关分析直接研究（原因是会得出两两间共计7*5个相关系数，无法分析出两组指标间的关系情况），因而使用典型相关分析进行研究。

• 2、理论

  典型相关分析是研究两组数据间的相关关系，此例中X组为7项，Y组为5项。典型相关分析思想在于：首先对数据提取出典型变量（即对于共12项的信息浓缩），然后在典型变量的基础进行分析。典型变量是对数据信息的浓缩提取，通常情况下典型变量会很少，通常为2~5个之间，便于对信息进行浓缩提取。

  完成典型变量提取之后，接着需要分别分析典型变量与X,或者Y之间的数学表达式关系，以及典型变量分别与X或者Y之间的关系情况；并且可结合具体情况对于典型变量进行命名。

  上述步骤已经提取出典型变量，并且进行命名，以及得到典型变量之间的相关关系情况，即X组和Y组之间的相关关系之后；还可以进一步进行典型冗余分析。

  典型冗余分析是指研究典型变量对于X组的信息提取量；也或者典型变量对于Y组的信息提取量情况。

  • 特别提示

  • 典型变量是成对出现的，比如当前两个典型变量分别是典型变量1和典型变量2；下述分析时会出现典型变量X1和典型变量Y1；典型变量X2和典型变量Y2。

• 3、操作

  • 本案例中X共有7项；Y共有5项。对应放入如下图：

    

• 4、SPSSAU输出结果

  

  此表格展示出典型变量的提取情况，上表中共显示有5个典型变量被提取出来，在进行F 检验时显示，其中仅2个典型变量是呈现出0.01水平的显著性，因此，最终应该以两个典型变量为准进行后续研究。并且第一个典型变量的相关系数值为0.763，第二个典型变量为0.706，相关系数值较高，说明典型变量之间有着紧密的正向相关关系。此步骤非常重要，共提取出2个典型变量，并且直接得出典型变量对的相关关系情况（即X组和Y组之间的相关关系情况）。

  通俗上讲，即可理解为总共X组7项指标，与Y组5项指标之间，最终可由两个典型变量对进行浓缩提取表示，而且此2个典型变量间的相关系数值均高于0.7，说明X组和Y组之间有着非常紧密的正向相关关系。

  • 特别提示

  • 上表格显示共提取出5个典型变量，因而接下来共3个表格均会以5个为准展示信息；但是仅2个典型变量呈现出显著性，因此，在具体分析时，仅分析对应的2个典型变量即可，其余3个没有呈现出显著性的典型变量不需要深入分析。

  • 典型变量是成对出现的，比如当前两个典型变量分别是典型变量1和典型变量2；下述分析时会出现典型变量X1和典型变量Y1；典型变量X2和典型变量Y2。

  

  上表格共展示出两项信息，分别是典型变量与X组7项指标的数学表达式（典型系数），以及典型变量与X组7项指标之间的相关关系（典型载荷系数）；

  • 从数学表达式上看可列出为如下：

  • 典型变量X1 = -0.015*x1-0.014*x2-0.002*x3-0.009*x4-0.004*x5-0.001*x6-0.002*x7

  • 典型变量X2 = 0.008*x1-0.010*x2+0.000*x3+0.005*x4+0.010*x5+0.004*x6-0.008*x7

  • 典型变量X3 = 0.037*x1-0.012*x2+0.000*x3-0.002*x4-0.007*x5+0.017*x6-0.002*x7

  • 典型变量X3 = -0.021*x1+0.011*x2+0.000*x3-0.019*x4+0.005*x5+0.013*x6-0.010*x7

  • 典型变量X5 = 0.028*x1-0.006*x2+0.000*x3-0.021*x4-0.002*x5-0.007*x6+0.019*x7

  • 从典型变量与X组7项指标的相关关系来看，其相关关系情况由典型载荷系数值表示，典型载荷系数绝对值越大说明该项与典型变量之间的相关关系越强：上述分析显示共有2个典型变量呈现出显著性，因而上表格的分析应该着重于研究此2个典型变量。典型变量X1与X组7项的相关关系（载荷系数）值分别是：-0.598，-0.751，-0.316，-0.296，-0.306，-0.277。典型变量X2与X组7项的相关系数（载荷系数）值分别是：0.311，-0.510，-0.118，0.039，0.773，-0.060，-0.163。

  如果用图示表示的话，如下面两图所示：

  

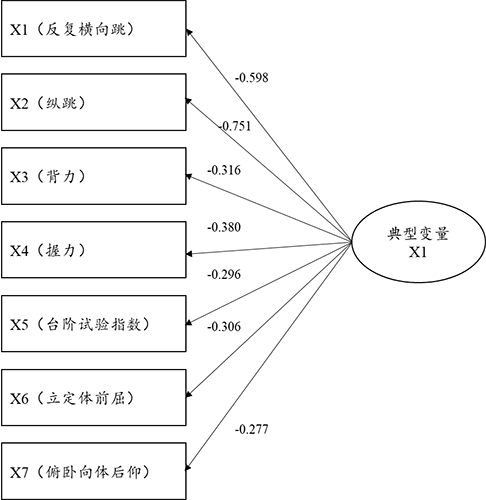
  上图非常直接的展示出第1个典型变量与7个指标之间的相关关系情况，明显的，典型变量与X1（反向横向跳）,X2（纵跳）的关系很强，即典型变量更多地提取X1（反向横向跳）,X2（纵跳）这两项的信息。

  

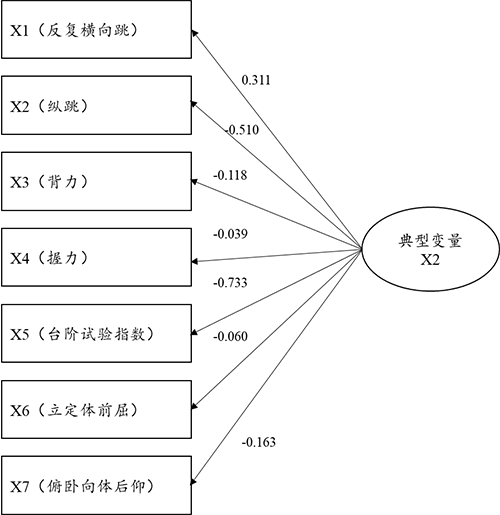
  上图非常直接的展示出第2个典型变量与7个指标之间的相关关系情况，明显的，典型变量与X2（纵跳），X5（台阶试验指数）的关系很强，即典型变量更多地提取X2（纵跳），X5（台阶试验指数）这两项的信息。

  

  上表格共展示出两项信息，分别是典型变量与Y组5项指标的数学表达式（典型系数），以及典型变量与Y组5项指标之间的相关关系（典型载荷系数）；

  • 从数学表达式上看可列出为如下：

  • 典型变量Y1 = 0.271*y1-0.001*y2-0.012*y3-0.010*y4-0.000*y5

  • 典型变量Y2 = -0.353*y1-0.004*y2-0.016*y3+0.002*y4-0.005*y5

  • 典型变量Y3 = 0.150*y1+0.001*y2+0.010*y3-0.021*y4-0.004*y5

  • 典型变量Y4 = 0.206*y1-0.003*y2+0.059*y3+0.035*y4+0.002*y5

  • 典型变量Y5 = -0.238*y1-0.000*y2+0.042*y3-0.042*y4+0.001*y5

  • 从典型变量与Y组5项指标的相关关系来看，其相关关系情况由典型载荷系数值表示，典型载荷系数绝对值越大说明该项与典型变量之间的相关关系越强：上述分析显示共有2个典型变量呈现出显著性，因而上表格的分析应该着重于研究此2个典型变量。典型变量Y1与Y组5项的相关关系（载荷系数）值分别是：0.866，-0.777，-0.564，-0.733，0.358。典型变量Y2与Y组5项的相关系数（载荷系数）值分别是：-0.286，-0.446，-0.131，0.017，-0.300。

  如果用图示表示的话，如下面两图所示：

  

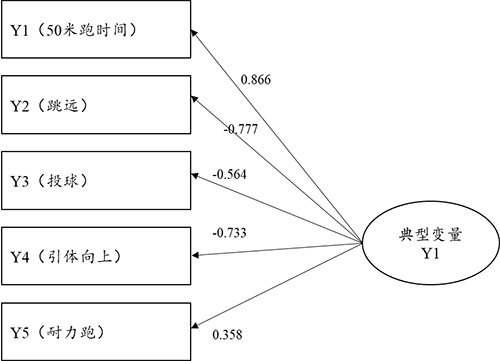
  上图非常直接的展示出第1个典型变量与5个指标之间的相关关系情况，明显的，典型变量与Y1（50米跑时间）,Y2（跳远）,Y3（投球）,Y4（引体向上）的关系很强，载荷系数绝对值均大于0.5，即典型变量更多地提取Y1（50米跑时间）,Y2（跳远）,Y3（投球）,Y4（引体向上）这4项的信息。

  

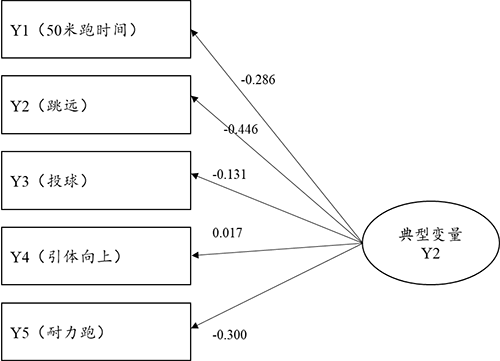
  上图非常直接的展示出第2个典型变量与5个指标之间的相关关系情况，明显的，典型变量与Y2（跳远）的关系很强，载荷系数绝对值为0.446，即典型变量更多地提取Y2（跳远）的信息。

  完成上述分析后，已经得出结论即：X组与Y组进行典型相关分析时，总共提取出两个典型变量对，典型变量对1更多地提取X1（反向横向跳）,X2（纵跳）这两项的信息；典型变量对2更多地提取X2（纵跳），X5（台阶试验指数）这两项的信息；典型变量对1更多地提取Y1（50米跑时间）,Y2（跳远）,Y3（投球）,Y4（引体向上）这4项的信息；典型变量对2更多地提取Y2（跳远）的信息。除此之外，典型变量对1之间的相关系数值为0.763，并且典型变量对2之间的相关系数值为0.703，典型变量相关系数值均高于0.7，意味着X组7项指标与Y组5项指标之间有着非常紧密的正向相关关系。

  

  接着进一步进行典型冗余分析，即了解典型变量对于研究数据的信息提取量情况。上表格展示5个典型变量分别对于X组或者Y组指标的信息提取情况；比如上表中典型变量X1可提取出X组7个指标20.325%的信息量，典型变量X1可提取出Y组5个指标11.826%的信息量。由于总共仅2个典型变量呈现出显著性，因而仅分析2项，而且只分析组内差异（即典型变量X与X组的信息提取，典型变量Y与Y组的信息提取）；

  从上表可以看出：典型变量X1和典型变量X2对于X组7项指标的信息提取量分别是20.325%和14.293%，共计34.62%；以及典型变量Y1和和典型变量Y2对于Y组5项指标的信息提取量分别是46.751%和7.760%，共计)54.51%。

• 5、文字分析

  • 使用典型相关分析去研究X组7项指标与Y组5项指标之间的典型相关分析，总共提取出两个典型变量对，典型变量对1更多地提取X1（反向横向跳）,X2（纵跳）这两项的信息；典型变量对2更多地提取X2（纵跳），X5（台阶试验指数）这两项的信息；典型变量对1更多地提取Y1（50米跑时间）,Y2（跳远）,Y3（投球）,Y4（引体向上）这4项的信息；典型变量对2更多地提取Y2（跳远）的信息。

  • 典型变量X1和典型变量X2对于X组7项指标的信息提取量分别是20.325%和14.293%，共计34.62%；以及典型变量Y1和和典型变量Y2对于Y组5项指标的信息提取量分别是46.751%和7.760%，共计)54.51%。

  • 最终分析可知：典型变量对1之间的相关系数值为0.763，并且典型变量对2之间的相关系数值为0.703，典型变量相关系数值均高于0.7，意味着X组7项指标与Y组5项指标之间有着非常紧密的正向相关关系。

  • 典型相关分析的信息量较大，建议可使用图示法，即将数字标识在图中，更好的呈现信息（包括典型变量分别与X或Y之间的关系情况，以及典型相关关系情况），比如本案例可画为两图如下：

  • 
  • 

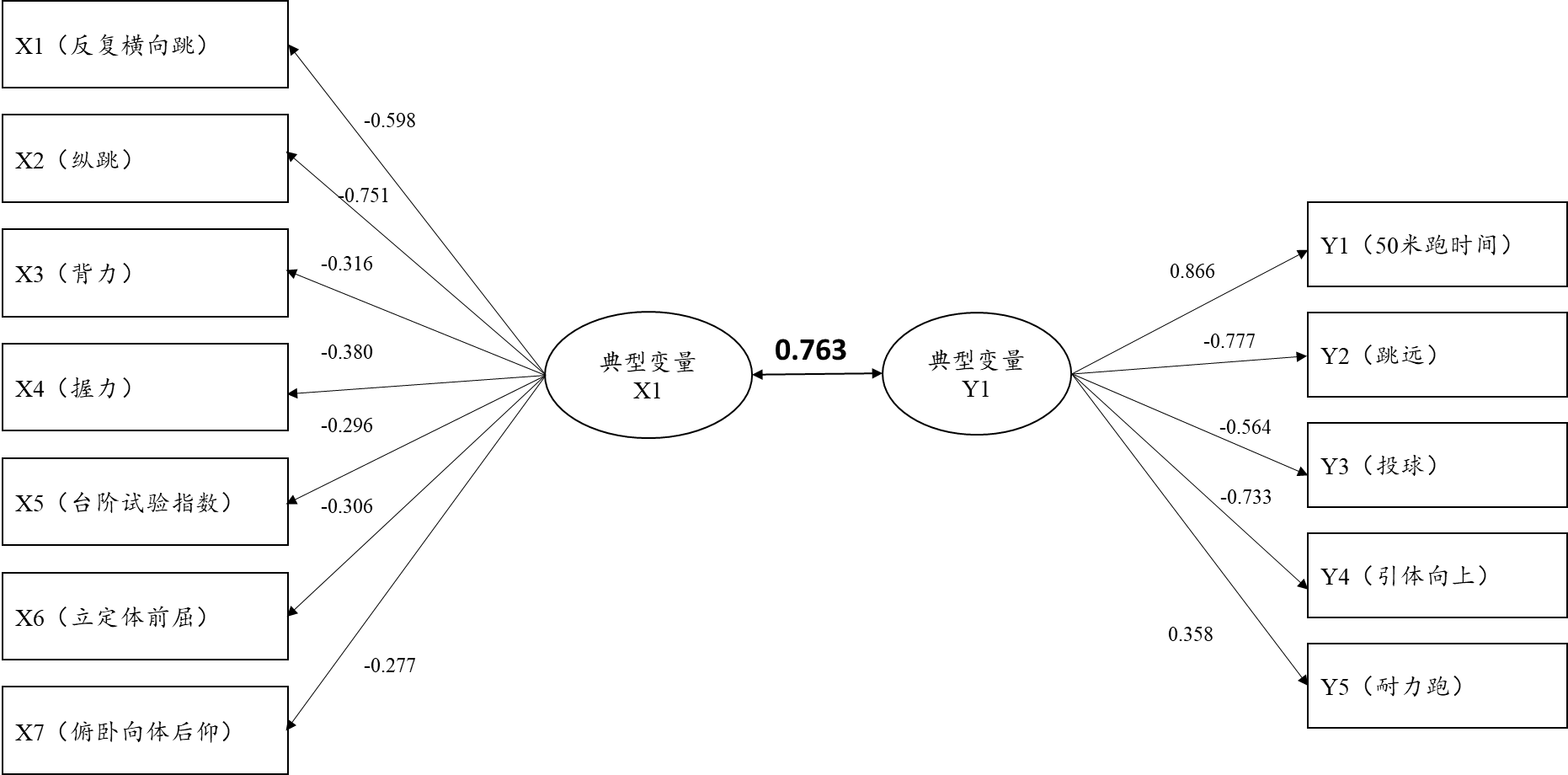
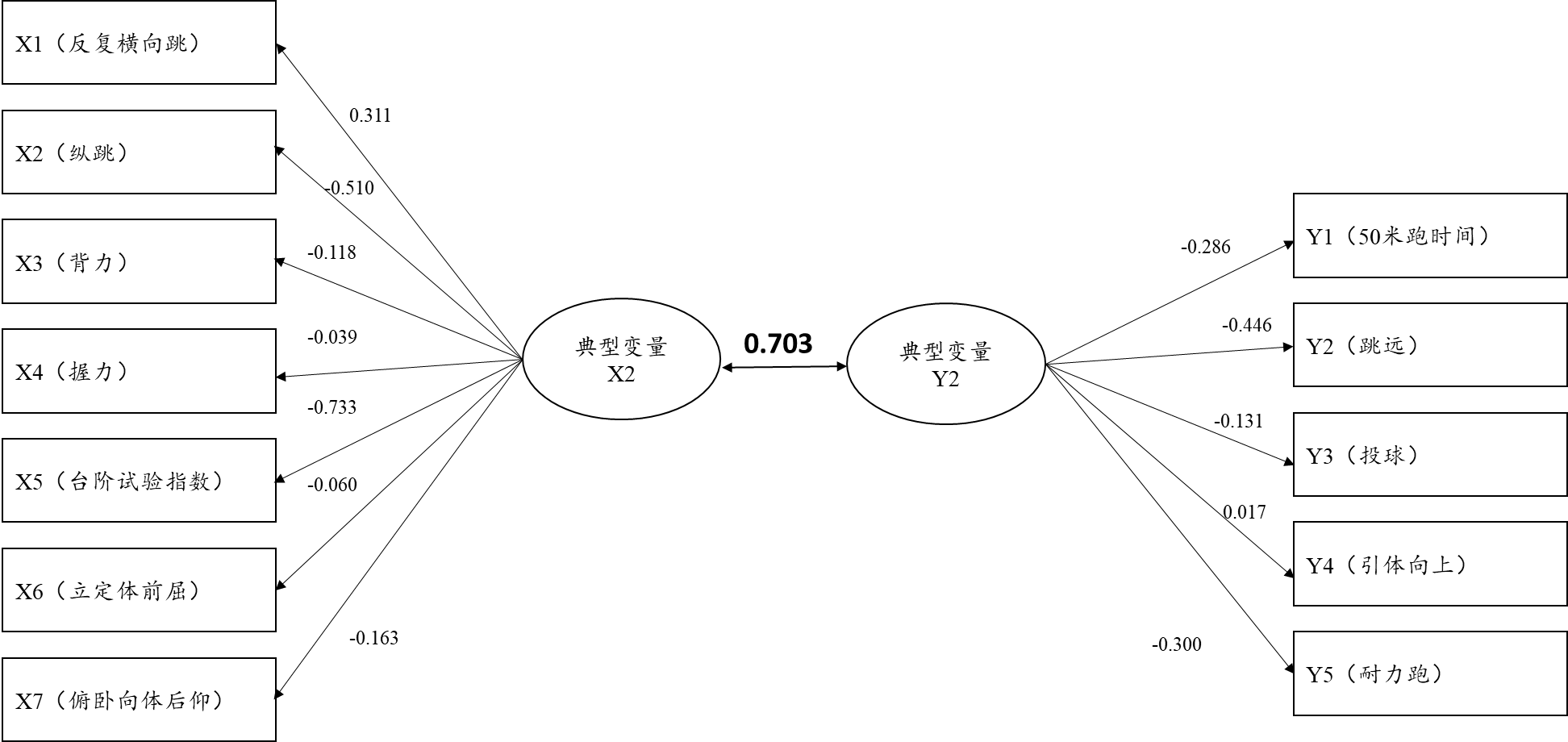
• 6、剖析

  • 典型变量是成对出现的，比如当前两个典型变量分别是典型变量1和典型变量2；分析时会出现典型变量X1和典型变量Y1；典型变量X2和典型变量Y2。

  • 典型相关分析共分为三个步骤:

  • 第一步是典型变量对的提取；

  • 第二步是典型变量分别与X组或者Y组之间的数学表达式，或相关关系（载荷系数）,并且可对典型变量进行命名；

  • 第三步是典型冗余分析，研究典型变量提取信息量情况。