TOPSIS法用于研究评价对象与‘理想解’的距离情况,结合‘理想解’(正理想解和负理想解),计算得到最终接近程度C值。熵权TOPSIS法核心在于TOPSIS,但在计算数据时,首先会利用熵值(熵权法)计算得到各评价指标的权重,并且将评价指标数据与权重相乘,得到新的数据,利用新数据进行TOPSIS法研究。
通俗地讲,熵权TOPSIS法是先使用熵权法得到新数据newdata(数据成熵权法计算得到的权重),然后利用新数据newdata进行TOPSIS法研究。
-
特别提示:
-
熵权TOPSIS实际上为熵权法后得到新数据,然后用新数据进行TOPSIS法研究。
熵权TOPSIS案例
-
1、背景
当前有6个国家经济技术开发区,分别在政务系统的4个指标上的评分值。数字越大表示指标越优。当前希望利用熵权TOPSIS法评价出6个开发区的政务系统排名情况。本例子的数据已经全部是正向指标,因此不需要进行正向化或逆向化处理;如果说指标中有负向指标;则需要让数据全部‘正向化’,针对正向指标做正向处理,负向指标做逆向处理。原始数据如下:
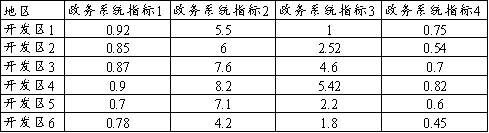
2、理论
熵权TOPSIS法分别涉及熵权法和TOPSIS法;熵权法计算各评价指标的权重值,然后利用权重值乘原始数据,得到newdata。系统利用newdata进行TOPSIS法进行计算,最终得到各评价对象的接近程序C值,用于判断和衡量评价对象的优劣排序等。
熵权法涉及以下专业术语,分别是信息熵值e,信息效用值d和权重系数w,信息熵值e和信息效用值d均为中间过程值;最终目的在于计算权重系数w值。
TOPSIS法涉及以下专业术语,分别是正理想解距离D+,负理想解距离D-,相对接近度C,正理想解A+和负理想解A-。正理想解距离D+是指数据与正理想解A+的距离;负理想解距离D-是指数据与负理想解A-的距离。正理想解A+是指每个评价指标的最优(一般是最大值),负理想解A-是指每个评价指标的最劣(一般是最小值)。相对接近度C=D- / (D+加上D-),该值越大意味着评价对象与最优解越接近,也即该值越大越好。
熵权TOPSIS分析的常见4个分析步骤如下:
-
Step1:数据正向化/逆向化处理;
-
如果数据中有逆向指标(数字越大反而越不好的意思),此时需要使用‘数据处理->生成变量’的‘逆向化’功能处理。让数据变成正向指标(即数字越大越好的意思)。
-
‘逆向化’的数据计算公式为:(Max-X)/(Max-Min),明显可以看出,针对逆向指标进行‘逆向化’处理后,数据就会变成正向指标。
-
Step2:数据标准化处理;
-
针对数据进行标准化处理,目的在于解决量纲化问题。常见的标准化处理方法有:‘归一化’,‘区间化’,‘均值化’等。
-
‘归一化’将所有数据压缩在0到1之间;
-
‘区间化‘将所有数据压缩在自己设定的区间;’
-
‘均值化’= 当前值 / 平均值。
-
一般而言,如果数据全部都大于0,建议使用‘均值化’;如果数据中有负数或者0,建议做‘区间化’让数据限定在一个区间(SPSSAU默认1~2之间);当然也可以考虑‘归一化’,让数据全部介于0~1之间。
-
具体标准化的处理方式有很多种,具体结合文献和自身数据选择使用即可。不同的处理方式肯定会带来不同的结果,但结论一般不会有太大的偏倚。
-
Step3:熵权法求权重,利用权重与数据相乘得到新数据newdata;
-
此步骤为SPSSAU的中间处理过程,SPSSAU默认输出熵权法得到的权重值,并且默认在内部算法过程中计算得到newdata。
-
Step4:利用TOPSIS法计算。
-
此步骤为SPSSAU的自动处理,默认输出TOPSIS相关的指标结果。
-
特别提示:
-
熵权TOPSIS实际上为熵权法后得到新数据,然后用新数据进行TOPSIS法研究。
3、操作
本案例数据中包括4个政务系统的评价指标,而且全部都是正向指标,因此不需要进行正向化或者逆向化处理。以及接着数据标准化解决量纲问题上,本例子使用‘均值化’处理方法。操作为数据处理->生成变量,如下图:
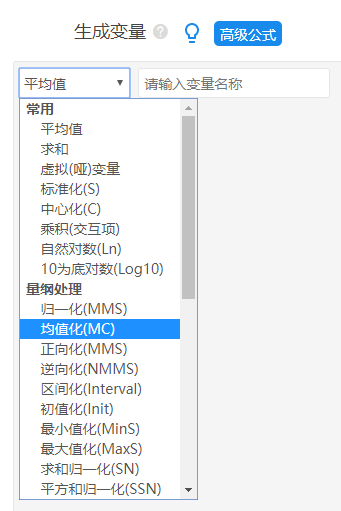
完成数据‘均值化’处理后,直接开始进行‘熵值TOPSIS法’分析,操作如下图:
4、SPSSAU输出结果
SPSSAU共输出3个表格,分别是:熵值法计算权重结果汇总;TOPSIS评价计算结果和正负理想解。
熵值法计算权重结果汇总展示出了熵值法后计算得到的权重;
TOPSIS评价计算结果和正负理想解这两个表格为TOPSIS评价相关的表格结果。
5、文字分析

上表格展示出4个政务系统指标的权重值,明显可以看出指标3的权重更大。但权重大小仅仅是过程值,熵值TOPSIS分析重心在于TOPSIS法计算出相对接近度。权重值与数据相乘,得到新数据newdata,这一过程是SPSSAU自动完成,利用newdata进行TOPSIS法计算。

从上表可知,利用熵权法后加权生成的数据(算法自动完成)进行TOPSIS分析,针对4个指标(MC_政务系统指标1, MC_政务系统指标2, MC_政务系统指标3, MC_政务系统指标4),进行TOPSIS评价,同时评价对象为6个(样本量数量即为评价对象数量);
TOPSIS法首先找出评价指标的正负理想解值(A+和A-),接着计算出各评价对象分别与正负理想解的距离值D+和D-。根据D+和D-值,最终计算得出各评价对象与最优方案的接近程度(C值),并可针对C值进行排序。
最终从上表可知:评价对象4,即开发区4,它的相对接近度C值最高为0.9995,因而说明开发区4在政务系统上的表现最优;其次是开发区3,相对接近度C起来0.8141。开发区1的政务系统表现最差。

正负理想解为计算正负理想距离值的过程值,一般不用过多关注。其代表某指标对应的最优或最劣值,在这里即为最大值或最小值。
6、剖析
涉及以下几个关键点,分别如下:
-
1.熵权TOPSIS实际上为熵权法后得到新数据,然后用新数据进行TOPSIS法研究;
-
2.熵权TOPSIS法一般分为四个步骤,如下:
-
Step1:数据正向化/逆向化处理;
-
Step2:数据标准化处理;
-
Step3:熵权法求权重,利用权重与数据相乘得到新数据newdata;
-
Step4:利用TOPSIS法计算。
疑难解惑
-
分析之前是否需要进行标准化、归一化、正向化或逆向化处理等?
-
如果原始数据中有负向指标(数字越大反而越不好的意思),需要针对此类指标先‘逆向化’处理。当确认所有指标均为正向指标(数字越大越好的意思)后,需要接着进标准化处理。
-
数据进行标准化处理目的在于解决量纲问题,标准化处理的方式有很多,常见是‘归一化’,‘区间化’,‘均值化’,‘求和归一化’,‘平方和归一化’等等非常多。如果指标数据全部都大于0,SPSSAU建议是使用‘均值化’处理,如果指标数据有小于或等于0的数据,SPSSAU建议使用‘区间化’(默认将数据压缩成1~2之间)。
-
如果分析数据中有负数或者0值如何办?
-
如果分析数据有负数或者0,这会导致无法进行熵值法计算,SPSSAU算法默认会进行‘非负平移’处理。SPSSAU非负平移功能是指,如果某列(某指标)数据出现小于等于0,则让该列数据同时加上一个‘平移值’【该值为某列数据最小值的绝对值+0.01】,以便让数据全部都大于0,因而满足算法要求。
-
面板数据如何进行熵值TOPSIS法?
-
熵值TOPSIS法的原理是先进行熵值法,然后再进行TOPSIS法。无论是面板或者非面板数据,均可正常进行熵值TOPSIS法研究,并不需要特别处理。
-
当然面板数据进行分析时,也可以先筛选出不同的年份,重复进行多次均可。
-
为什么分析样本量小于实际样本量?
-
如果分析时出现‘分析样本量’小于样本量,有3种可能。1是免费版(免费版仅分析前100行数据);2是做过‘筛选样本’功能(即主动设置只分析其中一部分数据);3是原始数据中有缺失数据(系统右上角‘我的数据’处可查看原始数据,也可下载原始数据等)。
-
SPSSAU熵权TOPSIS法时描述统计与描述分析结果不一致?
-
关于SPSSAU进行熵权TOPSIS时计算描述统计值的原理如下:
-
1、如果原始数据data中某列有小于等于0的数据,熵权topsis分析时,spssau会自动进行‘非负平移’处理【默认选中‘非负平移’复选框】,平移加上的数字为0.01【如果无此种情况则不处理】,得到newdata;
-
2、使用平移后的数据即newdata进行熵值法,并且得到权重 ;
-
3、使用newdata * 权重,得到newdata2;
-
4、使用newdata2进行topsis分析。
-
熵值Topsis时计算的平均值等是基于newdata进行,即可能是‘非负平移’后的数据。
-
分析结果中提示“预览前100项数据结果”?
-
SPSSAU中进行某些分析时,比如vikor/灰色关联法/topsis/熵权topsis/耦合协调度/综合指数时,并且分析样本量过大导致需要输出非常多结果时,此时结果仅输出前100项数据结果进行预览。此时可通过以下两步得到全部结果。
-
第1步:在‘开始分析’按钮右侧选中‘保存结果值’,系统将指标值存储在原始数据文档中,并且以不同的标题名称进行标识;
-
第2步:分析完成后,右上角‘我的数据’下载该数据文档,即将全部数据下载出来使用。
