-
相关分析描述分析项之间是否有关系,回归分析(线性回归分析)研究影响关系情况,回归分析实质上就是研究X(自变量,通常为量数据)对Y(因变量,定量数据)的影响关系情况,有相关关系不一定有回归影响关系。
分析步骤共为四步,分别是:
第一步:首先对模型情况进行分析
包括模型拟合情况(比如R 2为0.3,则说明所有X可以解释Y 30%的变化原因),模型共线性问题(VIF值小于5则说明无多重共线性),是否通过F 检验(F 检验用于判定是否X中至少有一个对Y产生影响,如果呈现出显著性,则说明所有X中至少一个会对Y产生影响关系)。
第二步:分析X的显著性
如果显著(p 值判断),则说明具有影响关系,反之无影响关系。
第三步:判断X对Y的影响关系方向
回归系数B值大于0说明正向影响,反之负向影响。
第四步:其它
比如对比影响程度大小(回归系数B值大小对比X对Y的影响程度大小)。
分析项 回归分析说明 网购满意度,重复购买意愿 网购满意度是否会影响到样本重复购买意愿?网购满意度越高,是否重复购买意愿也会越高? -
特别提示
-
如果多个量表题表示一个维度,可使用“生成变量”的平均值功能。将多个量表题合并成一个整体维度。
-
-
分析结果表格示例如下:
非标准化系数 标准化系数 t p VIF值 R 2 调整R 2 F B 标准误 Beta 常数 0.77 0.384 - 2.014 0.047* - 0.351 0.326 14.188** 分析项1 0.19 0.099 0.202 1.998 0.048* 1.320 分析项2 0.437 0.124 0.374 3.519 0.001** 1.320 分析项3 0.004 0.124 0.004 0.034 0.973 1.230 * p <0.05 ** p <0.01 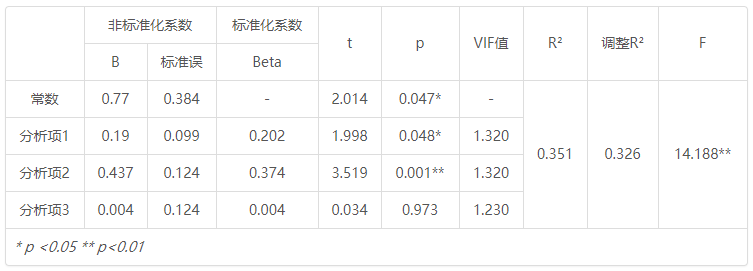
-
特别提示
-
F 对应的p 值是由*号表示(* p <0.05 ** p <0.01,如果F 值右上角没有*号,则说明F 值对应的p 值大于0.05)
-
回归分析之后,可对回归模型进行检验。可包括以下四项:
-
多重共线性:可查看VIF值,如果全部小于10(严格是5),则说明模型没有多重共线性问题,模型构建良好;反之若VIF大于10说明模型构建较差。如果呈现出共性问题,可使用逐步回归分析。
-
自相关性:如果D-W值在2附近(1.7~2.3之间),则说明没有自相关性,模型构建良好,反之若D-W值明显偏离2,则说明具有自相关性,模型构建较差。自相关问题产生时建议对因变量Y数据进行查看。
-
残差正态性:在分析时可保存残差项,然后使用“直方图”直观检测残差正态性情况,如果残差直观上满足正态性,说明模型构建较好,反之说明模型构建较差。如果残差正态性非常糟糕,建议重新构建模型,比如对Y取对数后再次构建模型等。
-
异方差性:可将保存的残差项,分别与模型的自变量X或者因变量Y,作散点图,查看散点是否有明显的规律性,比如自变量X值越大,残差项越大/越小,这时此说明有规律性,模型具有异方差性,模型构建较差。如果有明显的异方差性,建议重新构建模型,比如对Y取对数后再次构建模型等。
-
另外,如果回归分析出现各类异常,请查看数据中是否有异常值(可通过比如描述分析、箱线图、散点图等查看),找出异常值,并且处理掉异常值(使用“异常值”功能)。也或者使用稳健回归(Robust回归进行分析,Robust回归是专门处理异常值情况下的回归模型)。
SPSSAU操作截图如下:
-
回归分析案例
-
1、背景
比如想研究“淘宝客服服务态度”,“淘宝商家服务质量”分别与“淘宝商家满意度”,“淘宝忠诚度”之间的关系情况,此句话中明显的可以看出“淘宝客服服务态度”,“淘宝商家服务质量”这两项为 X;而“淘宝商家满意度”,“淘宝忠诚度”这两项为 Y。
-
特别提示
-
如果“淘宝客服服务态度”由几个题项表示,此时可使用“生成变量”->“平均值”功能,将几项概括成一个整体。
-
-
2、理论
回归分析是研究定量数据之间的影响关系情况,通常回归分析是放在相关关系分析之后。
针对回归分析:首先要F 检验,如果F 值右上角有*号,说明回归分析通过F 检验,即说明这个回归分析有意义可以做。然后通常需要看以下几个指标:R 2这个值在0~1之间,越大越好,它代表回归方程模型拟合的好坏,如果为0.5,说明有50%的点的都掉在回归方程上面,这个值没有好坏之分,一般只是希望越大越好。同时VIF值代表多重共线性,所有的VIF值均需要小于10,相对严格的标准是小于5。
接着分析具体X对Y的影响关系,首先判断有没有呈现出显著性,即p 值是否小于0.05,如果P <0.05则说明有影响关系,反之则说明没有影响关系。在说明已经有影响关系的前提下,具体是正向或是负向影响关系,则是通过“非标准化系数”或者“标准化系数”进行判断,大于0则说明是正向影响,反之则说明为负向影响。
-
特别提示
-
回归研究X对Y的影响;这里的X通常是定量数据,而非定类数据。如果X为定类数据,此时一般是作为控制变量(可能对模型有干扰因而放入的项),即放入模型,但并不对其进行分析。如果X为定类数据,而且还一定要分析它对Y的影响,此时应该进行虚拟变量(也称哑变量)【SPSSAU中的生成变量功能可进行设置】设置后再放入。
似想X如果为定类数据比如性别;Y为满意度;如果X呈现出显著性,即“越性别,越满意”这样的结论完全让人匪夷所思。所以以下建议:
-
如果X为定类数据,直接放入模型时,一般是不会对其进行分析,而仅仅是作为控制变量(可能对模型有干扰因而放入的项)放入就好。
-
如果X为定类数据,并且想分析X对Y的影响;比如相对于男性,女性有没有满意度更高。此时则需要进行虚拟变量(也称哑变量)【SPSSAU中的生成变量功能可进行设置】设置。
关于虚拟变量的更多理论知识,建议参考:
-
-
3、操作
-
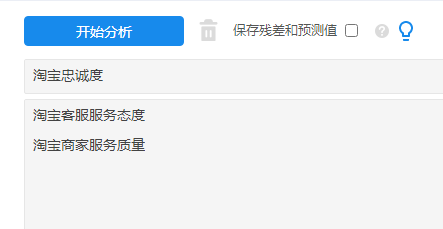
“淘宝客服服务态度”,“淘宝商家服务质量”这两项为X;而“淘宝忠诚度”为Y。操作如下图:
-
特别提示
-
专业用户如果有特别要求,比如希望保存残差值和预测值,则可将“保存残差和预测值”这项打勾即可,通常情况并不需要。
-
-
-
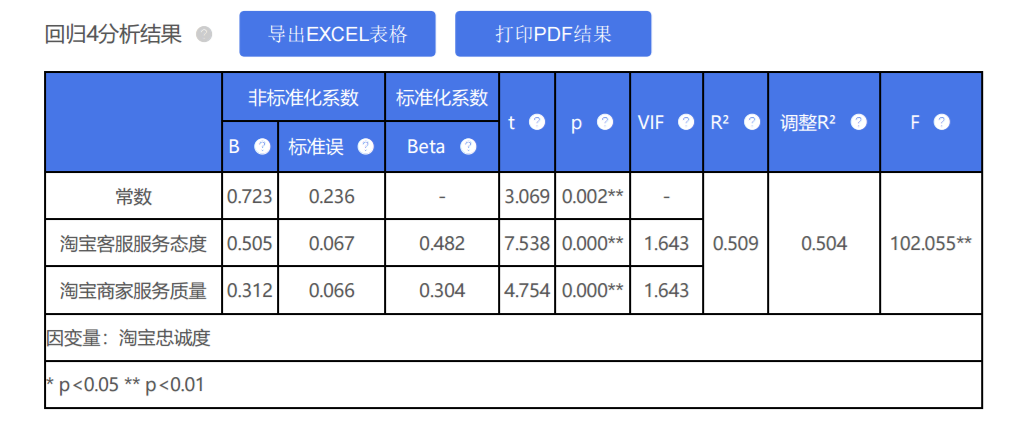
4、SPSSAU输出结果
-
5、文字分析
-
上表使用回归分析去研究“淘宝客服服务态度”,“淘宝商家服务质量”对于“淘宝忠诚度”的影响关系情况。从上表可以看到:
-
模型通过F 检验(p <0.01),意味着研究模型具有意义,“淘宝客服服务态度”,“淘宝商家服务质量”这两项中至少一项,会对“淘宝忠诚度”产生影响关系。模型 R 2值为0.509,意味着“淘宝客服服务态度”,“淘宝商家服务质量”这两项可以解释“淘宝忠诚度”的50.9%变化原因。以及模型公式为:淘宝忠诚度=0.723 + 0.505*淘宝客服服务态度 + 0.312*淘宝商家服务质量。另外,针对模型的多重共线性进行检验发现,模型中VIF值全部均小于5,意味着不存在着共线性问题,模型较好。具体分析可知:
-
“淘宝客服服务态度”的回归系数值为0.505,并且呈现出0.01水平的显著性(p <0.01),意味着“淘宝客服服务态度”会对“淘宝忠诚度”产生显著的正向影响关系。以及“淘宝商家服务质量”的回归系数值为0.312,并且呈现出0.01水平的显著性( p <0.01),意味着“淘宝商家服务质量”会对“淘宝忠诚度”产生显著的正向影响关系。
-
总结分析可知:“淘宝客服服务态度”,“淘宝商家服务质量”这两项全部均会对淘宝忠诚度产生显著的正向影响关系。
-
-
6、剖析
通常来说,回归分析之前还需要使用相关分析研究相关关系,首先要保证有相关关系之后,再进行回归分析较为科学。R 2值越大越好,但此指标相对来讲重要性不是特别高,更多关注于X的显著性,便于讨论X对于Y的影响关系情况。
-
7 、进一步模型分析
-
回归分析之后,可对回归模型进行检验。可包括以下四项:
-
多重共线性:可查看VIF值,如果全部小于10(严格是5),则说明模型没有多重共线性问题,模型构建良好;反之若VIF大于10说明模型构建较差。
-
自相关性:如果D-W值在2附近(1.7~2.3之间),则说明没有自相关性,模型构建良好,反之若D-W值明显偏离2,则说明具有自相关性,模型构建较差。
-
残差正态性:在分析时可保存残差项,然后使用“直方图”直观检测残差正态性情况,如果残差直观上满足正态性,说明模型构建较好,反之说明模型构建较差。
-
异方差性:可将保存的残差项,分别与模型的自变量X或者因变量Y,作散点图,查看散点是否有明显的规律性,比如自变量X值越大,残差项越大/越小,这时此说明有规律性,模型具有异方差性,模型构建较差。
-
疑难解惑
-
控制变量如何分析?
-
控制变量指可能干扰模型的项,比如年龄,学历等基础信息。从软件角度来看,并没有“控制变量”这样的名词。“控制变量”就是自变量,所以直接放入“自变量X”框中就好。
-
另外,控制变量一般是定类数据,理论上控制变量需要作“虚拟(哑)变量”设置,但实际研究中很少这样做而是直接放入模型中,可能原因是“控制变量”并非核心研究项,所以不用考虑太过复杂。
-
R 2值多少合适?
-
R平方值表示模型拟合能力的大小,比如0.3表示自变量X对于因变量Y有30%的解释能力。这个值介于0~1之间,越大越好。但实际研究中并没有固定的标准,有的专业0.1甚至0.05这样都可以,但有的专业却常常出现0.8以上。一般情况下只需要报告此值即可,不用过多关注其大小,原因在于多数时候我们更在乎X对于Y是否有影响关系即可。
-
针对问卷量表数据,几个题表示一个维度,如何处理?
-
比如有两个题“我愿意向朋友推荐SPSSAU”,“我有需要会再来使用SPSSAU”,此两个题是“忠诚度”的体现。但现在需要“忠诚度”这个整体,而不是具体两个标题,此时如何办呢?
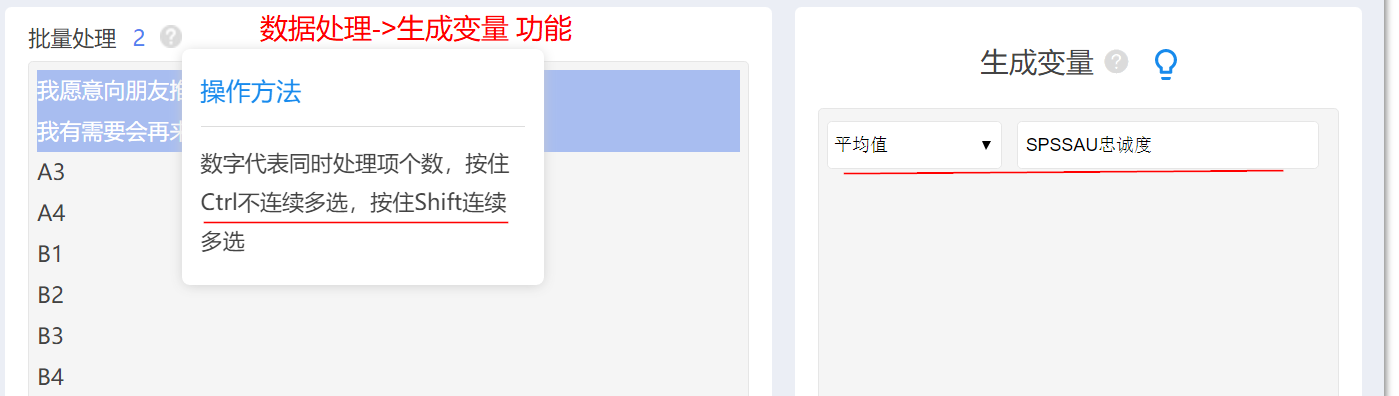
-
有相关关系,但是显示没有回归影响关系?
-
可量看此页面详细说明: https://www.spssau.com/helps/otherdocuments/correlationregression.html
-
多重共线性问题?
-
VIF值用于检测共线性问题,一般VIF值小于10即说明没有共线性(严格的标准是5),有时候会以容差值作为标准,容差值=1/VIF,所以容差值大于0.1则说明没有共线性(严格是大于0.2),VIF和容差值有逻辑对应关系,因此二选一即可,一般描述VIF值。
-
如果出现多重共线性问题,一般可有3种解决办法,一是使用逐步回归分析(让模型自动剔除掉共线性过高项);二是使用岭回归分析(使用数学方法解决共线性问题),三是进行相关分析,手工移出相关性非常高的分析项(通过主观分析解决),然后再做线性回归分析。
-
回归分析缺少Y
-
回归分析是研究X对于Y的影响。有时候由于问卷设计问题,导致直接缺少了Y(没有设计对应的问卷题项),建议可以考虑将X所有题项概括计算平均值来表示Y。(使用“ 生成变量”的 平均值功能)(另提示:如果问卷中并没有设计出Y对应的题项,没有其它办法可以处理)
-
影响关系的大小,那个自变量影响更大一点?
-
如果说自变量X已经对因变量Y产生显著影响(P< 0.05),还想对比影响大小,建议可使用标准化系数( Beta)值的大小对比影响大小,Beta值大于0时正向影响,该值越大说明影响越大。Beta值小于0时负向影响,该值越小说明影响越大。
-
回归分析之前是否需要先做相关分析?
-
一般来说,回归分析之前需要做相关分析,原因在于相关分析可以先了解是否有关系,回归分析是研究有没有影响关系,有相关关系但并不一定有回归影响关系。当然回归分析之前也可以使用散点图直观查看数据关系情况等。
-
提示“共线性严重请使用岭回归等”?
-
如果提示共线性严重时,可能有以下原因所致。
-
第一:自变量之间的相关关系非常强;
-
第二:虚拟(哑)变量时放入所有虚拟变量项;
-
第三:样本个数太少,比如低于10个;
-
第四:某个自变量出现数字恒定,比如某个自变量全部都为数字1。
-
检查办法和解决办法:
-
对因变量和自变量进行相关分析,如果有发现相关性非常高的变量时,将其在回归模型中移出;
-
如果是虚拟(哑)变量问题,请参考此页面:
-
如果是样本数量太少,加大样本量即可;
-
同时可使用描述分析检查是否自变量的数字恒定,如果是,需要将该自变量从回归模型中移出去。
-
F 值括号里面的两个值分别是什么?
-
如果是F 值想计算得到p 值,需要提供两个自由度值df 1和df 2。一般情况下,df 1等于自变量数量;df 2等于样本量 - (自变量数量+1)。此两个值仅为中间过程值,规范格式上需要写成这样而已,无其它实际意义。
-
因变量Y只能放1个但是我有多个如何办?
-
比如有两个题“我愿意向朋友推荐SPSSAU”,“我有需要会再来使用SPSSAU”,此两个题是“忠诚度”的体现。可使用SPSSAU【数据处理->生成变量(平均值)】功能完成。通常将多个题概括成一个整体之后,则可以进行相关分析、回归分析、方差分析等(以整体进行,而不是以题项分别进行)。
-
单独一个X进行回归有影响,多个X一起就没有影响?
-
有时候会出现只放一个X影响Y时,显示有显著影响关系;如果放多个X同时在模型里就显示没有显著影响关系。这种情况非常正常,放入多个X的时候可能有 ‘竞争’关系,并且多个X放入的时候有可能出现共线性问题等。研究者结合实际情况进行即可,相对来讲一次性放多个X的情况较多,相当于模型包括多个X;而一次放一个重复多次,相当于是多个模型。
-
常数项值很大或者很小?
-
常数项无实际意义,包括其对应的显著性值等均无实际意义,只是数学角度上一定存在而已。
-
回归系数非常非常小或者非常非常大?
-
如果说数据的单位很大,不论是自变量X还是因变量Y;此种数据会导致结果里面的回归系数出现非常非常小,也或者非常非常大。此种情况是正常现象,但一般需要对数据进行统一取对数处理,以减少单位问题带来的‘特别大或特别小的回归系数’问题。
-
SPSSAU中的coefPlot图?
-
SPSSAU在多个研究方法(包括线性回归,OLS回归,二元logit等)均提供coefPlot图,coefPlot展示具体的回归系数值和对应的置信区间,可直观查看数据的显著性情况,如果说置信区间包括数字0则说明该项不显著,如果置信区间不包括数字0则说明该项呈现出显著性。
-
SPSSAU中输出容忍度值?
-
SPSSAU默认输出VIF值和容忍度值进行共线性诊断,容忍度值=1/VIF值,一般情况下VIF值小于10(严格是小于5)则说明没有共线性问题,对应容忍度值的标题是大于0.1(严格是大于0.2)则说明没有共线性问题。
-
线性回归时进行异常值诊断?
-
针对线性回归进行异常点诊断,SPSSAU提供‘学生化残差’,‘cook距离 ’和‘杠杆值’共三项指标,保存‘异常点信息’后,可在原始数据中查看具体该3个指标值。如果需要除掉异常值,可进行‘筛选样本’功能,筛选正常数据后进行分析。
-
与此同时,SPSSAU输出结果中提供‘异常点分析’,当发现可能有潜在异常点时,可尝试使用‘筛选样本’功能,筛选出正常数据后分析,并且进行结果对比选择使用等。
-
SPSSAU线性回归没有保存异常值?
-
当进行线性回归时,选中‘异常点诊断’或‘异常点信息保存’,该两项参数仅在分析样本量小于等于1000时生效,如果样本量超过1000且选中该两项,系统默认也不进行。
-
简单回归和多元回归的区别是什么?
-
当放入X个数为1个时,通常称其为一元回归或者简单回归,当放入X超过1个时,则称作多元回归。此种称呼在线性回归或者logistic回归中均一致。
