中介效应案例

• 1、背景

  当前有一个研究（样本量为200），自变量有两个，中介变量共有3个，因变量有一个，希望研究自变量X对于因变量Y的影响时，3个中介变量是否会起到桥梁中介作用。

  变量类型	名称
  自变量	X1,X2
  中介变量	M1,M2,M3
  因变量	Y

• 2、理论

  在研究中介作用时，其有多种做法，常见做法有两种，第一种是因果逐步回归检验法，使用分层回归（SPSSAU》进阶方法）进行研究。第二种是乘积系数法检验法，其具体做法上可分为Sobel检验和Bootstrap抽样法检验；第一种做法相对简单易懂因而得到广泛使用，但是其检验效能相对较低，因此当前更适合的做法是使用第二种即乘积系数检验法，并且使用Bootstrap抽样法进行中介作用检验。

  中介作用的检验基本理论数学模型如下：

  

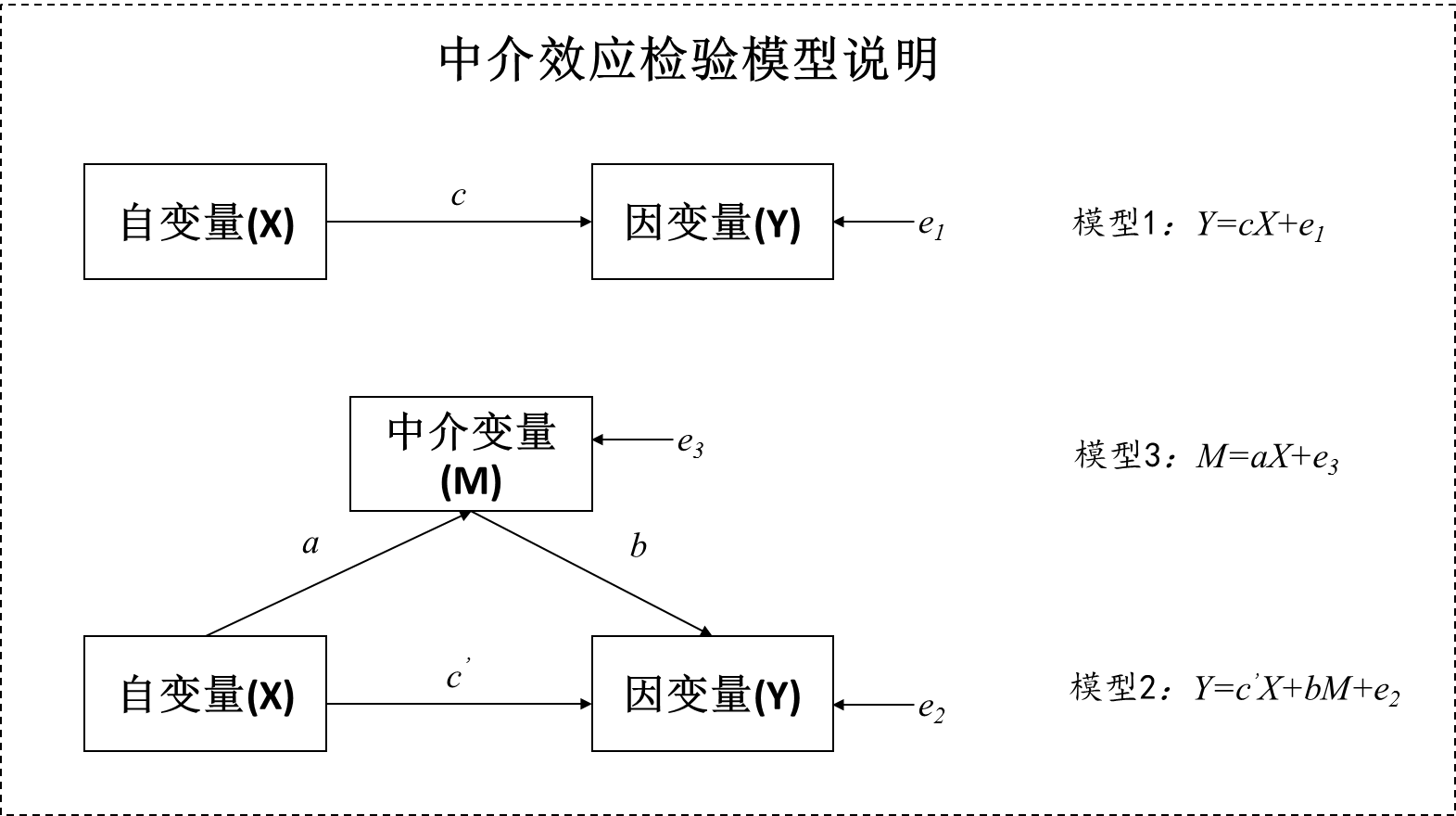
  中介作用共分为3个模型。针对上图说明如下：

  • 模型1：自变量X和因变量Y的回归分析；目的为得到总效应c值；

  • 模型2：自变量X，中介变量M和因变量Y的回归分析；目的是得到直接效应c’值，以及中间效应过程值b；

  • 模型3：自变量X和中介变量M的回归分析；目的是得到中间效应过程值a。

  • 模型1和模型2的区别在于，模型2在模型1的基础上加入了中介变量M。

  上图中回归系数a和回归系数b的乘积项（a*b）称为间接效应，如果其呈现出显著性，那么就说明具有中介作用，反之不具有显著性，则说明不具有中介作用。检验a*b的显著性用于判断是否具有中介作用，这种做法即称为乘积系数检验法。而具体Bootstrap抽样法检验是指a*b这个回归系数的95%置信区间是否包括数字0；如果说95%置信区间不包括数字0，则说明具有中介作用；如果说95%置信区间包括数字0，即说明没有中介作用。

  除此之外，总效应 = 直接效应 + 间接效应，如果在分析完中介作用后，还需要深入分析各种效应的占比，可结合此公式进行计算即可。

  • 特别提示：

  • SPSSAU直接将中介作用的检验过程自动化，并提供出上述提及模型的结果值等，研究者只需要关注“间接效应分析”中的检验结果即可。

• 3、操作

  本例子中包括2个自变量，3个中介变量；那么需要按X的个数（2个）即重复两次即可。第一次的时候将X1放入自变量，X2放入控制变量中；第二次的时候将X2放入自变量，X1放入控制变量中。

  从理论模型来看，X1放入自变量X2放入控制变量；或者X2放入自变量X1放入控制变量；单纯从中介作用的3个模型结果来看是完全一模一样的；但是涉及的中介作用检验不一样而已。

  本次自变量X为2个，先针对X1作为自变量，X2作为控制变量时的操作截图如下：

  

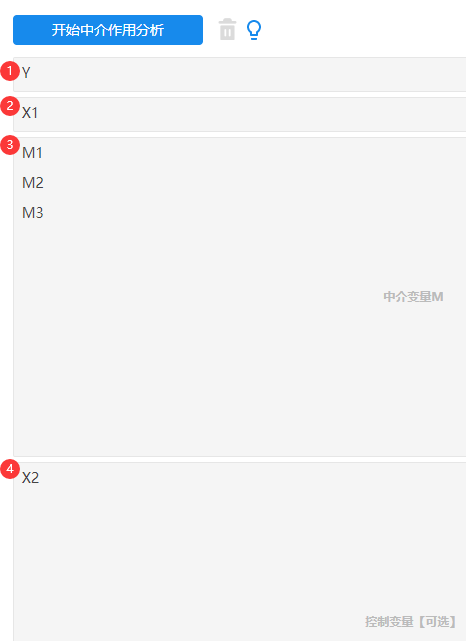
• 4、SPSSAU输出结果

  SPSSAU共输出4类表格；第一是“中介效应模型检验”表格；第二是“效应分析过程汇总”表格；第三是“间接效应分析”表格；第四是“中介效应模型检验-简化格式”表格。

  本次研究是中介变量共分为三个分别是M1,M2和M3；因此自变量X1与中介变量的回归关系共分为3个模型。即“中介效应模型检验”表格共包括1+1+3=5个模型。“中介效应模型检验”表格为初始的模型结果值；中介作用分析时，需要结合数学理论将初始结果值整理成“效应分析过程汇总”表格和“间接效应分析”表格。

  真实研究时，基本上均针对“效应分析过程汇总”表格和“间接效应分析”表格分析即可。

• 5、文字分析

  

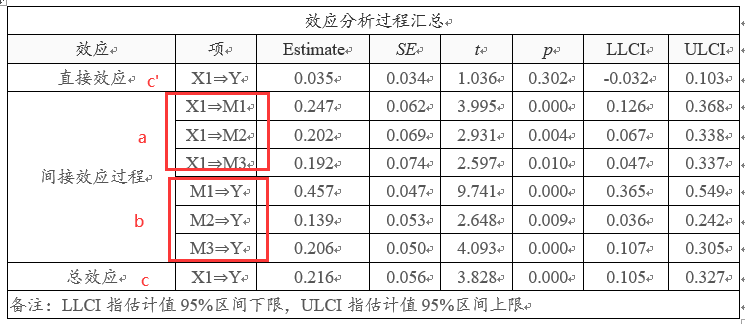
  从上表格可知：总效应来看，X1对于Y的总效应呈现出0.01水平的显著性(t =3.828,p =0.000 <0.01)；从直接效应来看，X1对于Y并没有产生显著影响关系(t =1.036,p =0.302>0.05)，即说明直接效应不存在。

  效应分析过程汇总值列出数学模型中的a和b值，即a表格自变量对中介变量的影响值；b表示中介变量对于因变量的影响值；由于本案例中涉及3个中介变量，因此a值为3个，b值也是3个。间接效应共分为三项，分别是X1通过M1,M2或M3再去影响Y。如下表格所示：

  

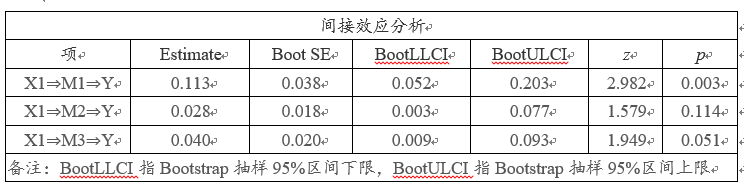
  上表格中X1⇒M1⇒Y的回归系数值为0.113，该值a*b=0.247*0.457。类似的X1⇒M2⇒Y时的回归系数值为0.028=0.202*0.139。类似的X1⇒M3⇒Y时的回归系数值为0.040=0.192*0.206。

  使用Bootstrap抽样检验法进行中介作用研究，抽样次数为5000次，结果显示：针对X1对于Y影响时，M1的中介作用检验， a*b检验系数值95%区间并不包括数字0(95% CI:0.052~0.203)，因而说明X1对于Y影响时，M1具有中介作用。X1首先会对M1产生影响，然后通过M1再去影响Y

  针对X1对于Y影响时，M2的中介作用检验， a*b检验系数值95%区间并不包括数字0(95% CI:0.003~0.077)，因而说明X1对于Y影响时，M2具有中介作用。X1首先会对M2产生影响，然后通过M2再去影响Y。

  针对X1对于Y影响时，M3的中介作用检验， a*b检验系数值95%区间并不包括数字0(95% CI:0.009~0.093)，因而说明X1对于Y影响时，M3具有中介作用。X1首先会对M3产生影响，然后通过M3再去影响Y。此处对应的p 值为0.051>0.05，但是95%区间不包括数字0，因此应该以有中介作用作为最终结论。

  除此之外，中介作用检验时有一个恒等式即：总效应c=直接效应c’+间接效应a*b。本案例时也是这样，即0.216=0.035+0.113+0.028+0.040。如果需要进一步分析效应占比的话，可列表格如下：

  效应	项	回归估计值	效应占比
  直接效应	X1⇒Y	0.035	16.20%
  间接效应	X1⇒M1⇒Y	0.113	52.31%
  	X1⇒M2⇒Y	0.028	12.96%
  	X1⇒M3⇒Y	0.04	18.52%
  总效应	X1⇒Y	0.216	100.00%

• 6、剖析

  涉及以下几个关键点，分别如下：

  • 中介作用分析前是否需要自变量对因变量产生影响？

  • 使用乘积系数法进行中介作用分析时，并不要求自变量对于因变量产生影响关系。即并不要求直接效应呈现出显著性。

  • 中介作用是否需要首先进行标准化处理？

  • 进行标准化或中心化处理，通常是出于共线性问题的考虑而进行。事实上并无其它帮助，研究者可以进行标准化处理，当然如果没有共线性问题不进行也不妨。可使用数据处理》生成变量功能进行处理。

  • 有调节的中介作用如何进行？

  • 如果是分析有调节的中介作用，其重心是在中介作用这里，先进行中介作用分析（此时完全不考虑调节作用，当然也可以把调节变量或交互项纳入控制变量中即可）；然后再进行调节作用分析即可。类似地，如果研究有中介的调节作用也是一样的处理，先处理调节作用，再处理中介作用。分析时完全分开进行中介作用或者调节作用即可。