-
面板数据(panel data)是指不同对象在不同时间上的指标数据。比如100个公司,每个公司有5年的数据,即100*5=500行数据。如下图:每个公司编号下有5年(2011~2015)的数据。在实际研究中,需要首先告诉SPSSAU,研究对象(公司编号)和时间点(年份)分别是什么。
公司编号 年份 财务指标1 财务指标2 财务指标3 财务指标4 ... 1 2011 1 2012 1 2013 1 2014 1 2015 2 2011 2 2012 2 2013 2 2014 2 2015 ... ... ...... ...... 如果100个公司,每个公司5年,总计500行并没有缺失数据,此种数据叫平衡数据。如果出现个别公司少了某个的数据,此种数据叫不平衡数据。
面板数据进行回归影响关系研究时,即称为面板模型(面板回归)。一般情况下,面板模型可继续分为三种类型,分别是FE模型,POOL模型(就是普通的OLS回归)和RE模型。最终应该选择哪个模型,可通过各个检验进行判断。SPSSAU分别进行F检验,BP检验和Hausman检验(豪斯曼检验),以判断出最终应该使用哪个模型(现实研究中,可能还有其它的检验方法)。
F检验用于判断FE和POOL模型,如果p 值小于0.05,则应该以FE模型为准。BP检验用于判断RE和POOL模型,如果p 值小于0.05,则应该以RE模型为准。Hausman检验用于判断FE和RE模型,如果p 值小于0.05,则应该以FE模型为准。结合三个检验,最终判断出哪个模型最优。
检验类型 检验目的 检验值 检验结论 F检验 FE模型和POOL模型比较选择 p 值<0.05 FE模型 BP检验 RE模型和POOL模型比较选择 p 值<0.05 RE模型 Hausman检验 FE模型和RE模型比较选择 p 值<0.05 FE模型 -
除了F检验,BP检验和经典的Hausman检验(豪斯曼检验)外,可能还有其它检验,但SPSSAU暂未提供。
-
如果是经济类数据,多数情况下FE模型更优,因而很多研究直接默认不检验直接使用FE模型;
特别提示
-
面板模型案例
-
1、背景
当前有一份城镇GDP相关的数据,共有9个地区分别11年(2008~2018)的数据,无缺失数据因而为9*11=99个样本。数据中包括X1(城乡居民年末储蓄存款), X2(年末常住人口), X3(城镇化率), X4(教育支出)共4个自变量,因变量为GDP。现希望研究4个自变量对于GDP的影响情况。以及数据值较大,为防止异方差问题因而进行过取对数处理。
-
2、理论
面板模型可继续分为三种类型,分别是FE模型,POOL模型(就是普通的OLS回归)和RE模型。最终应该选择哪个模型,可通过各个检验进行判断。SPSSAU分别进行F检验,BP检验和Hausman检验(豪斯曼检验),以判断出最终应该使用哪个模型(现实研究中,可能还有其它的检验方法)。
F检验用于判断FE和POOL模型,如果p 值小于0.05,则应该以FE模型为准。BP检验用于判断RE和POOL模型,如果p 值小于0.05,则应该以RE模型为准。Hausman检验用于判断FE和RE模型,如果p 值小于0.05,则应该以FE模型为准。结合三个检验,最终判断出哪个模型最优。
检验类型 检验目的 检验值 检验结论 F检验 FE模型和POOL模型比较选择 p 值<0.05 FE模型 BP检验 RE模型和POOL模型比较选择 p 值<0.05 RE模型 Hausman检验 FE模型和RE模型比较选择 p 值<0.05 FE模型 -
特别提示
-
除了F检验,BP检验和经典的Hausman检验(豪斯曼检验)外,可能还有其它检验,但SPSSAU暂未提供。
-
如果是经济类数据,多数情况下FE模型更优,因而很多研究直接默认不检验直接使用FE模型;
-
一般情况下,三种模型的选择上有区别,但结论上一般区别不会太大。
-
-
3、操作
本例子的数据格式如下:
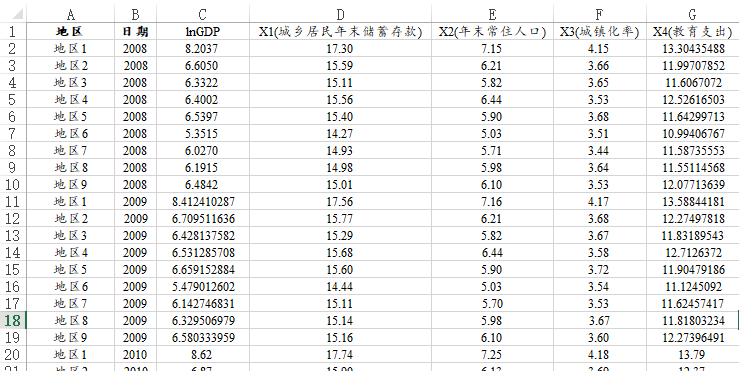
研究4个X对于GDP的影响,并且需要标识出面板数据,分别将地区和日期放入对应的‘个体ID’和‘时间’框中。
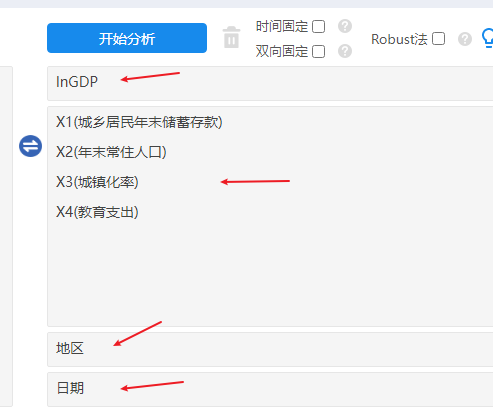
-
4、SPSSAU输出结果
SPSSAU共输出3类表格,分别是检验汇总表格,面板模型结果汇总表格,模型中间过程结果表格。
-
5、文字分析

面板模型涉及3个模型分别是混合POOL模型、固定效应FE模型和随机效应RE模型,首先进行模型检验,便于找出最优模型,从上表可知:F 检验呈现出5%水平的显著性F (8,86)=0.000,p =0.000 <0.05,意味着相对POOL模型而言,FE模型更优。BP检验呈现出5%水平的显著性χ2 (1)=155.600,p =0.000< 0.05,意味着相对POOL模型而言,RE模型更优。Hausman检验呈现出5%水平的显著性χ2 (4)=71.995,p =0.000< 0.05,意味着相对RE模型而言,FE模型更优。综合上述分析,SPSSAU建议最终以FE模型作为最终结果。
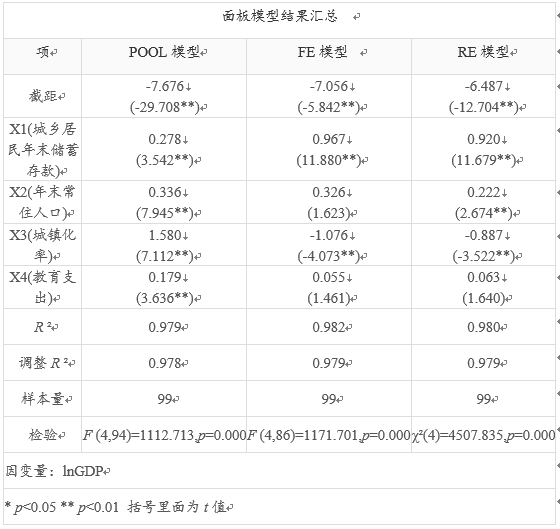
最终检验显示以FE模型结果为准。从表格中可以看出:针对X1(城乡居民年末储蓄存款)而言,其呈现出0.01水平的显著性(t =11.880,p =0.000 <0.01),并且回归系数值为0.967>0,说明X1(城乡居民年末储蓄存款)对GDP会产生显著的正向影响关系。
针对X2(年末常住人口)而言,其并没有呈现出显著性(t =1.623,p =0.108>0.05),因而说明X2(年末常住人口)对GDP不会产生影响关系。
针对X3(城镇化率)而言,其呈现出0.01水平的显著性(t =-4.073,p =0.000 <0.01),并且回归系数值为-1.076<0,说明X3(城镇化率)对GDP会产生显著的负向影响关系。
针对X4(教育支出)而言,其并没有呈现出显著性(t =1.461,p =0.148>0.05),因而说明X4(教育支出)对GDP不会产生影响关系。
-
6、剖析
涉及以下几个关键点,分别如下:
-
一般情况下,三种模型的选择上有区别,但结论上一般区别不会太大;
-
面板数据时,如果数据值过大,一般会取对数处理。
-
除了F检验,BP检验和经典的Hausman检验(豪斯曼检验)外,可能还有其它检验,但SPSSAU暂未提供。
-
如果是经济类数据,多数情况下FE模型更优,因而很多研究直接默认不检验直接使用FE模型;
-
疑难解惑
-
出现质量异常?
-
如果提示质量异常,通常是由于数据格式不对,请检查是否按照正确的面板数据格式规范数据。也或者说变量之间有着高度的共线性(相关系数大于0.9),也或者缺失数据过多导致有效样本太少等原因。建议分别使用相关分析检验数据的相关关系情况,使用描述分析检验有效样本量情况。
| 项 | 可能原因 | 检查或解决办法 |
| 0 | 通用问题(相关系数接近1或0,样本量过少) | 按通用问题对应的解决办法 |
| 1 | 数据格式不对 | 查看数据格式例子 |
-
上传到SPSSAU的数据显示为NULL?
-
比如股票代码为“000112”,有可能会被当成文字因而处理成NULL值,建议在EXCEL里面此类本身是数字但显示成文字的数据强制转换成数字。比如“2018年1月1日”这样的日期会被当成文字处理成NULL值,建议在EXCEL里面使用比如year、month函数提取出有效的年月数据后再上传到SPSSAU中。具体可参考上传数据页面说明: https://www.spssau.com/helps/basics/uploaddatas.html
-
先做相关分析后再做面板模型。
-
一般情况下,可以做相关分析研究自变量X与因变量Y之间的相关关系,便于了解数据之间的相关关系情况。有时也可分别筛选出各个不同时间点(比如不同年份)数据,分别做多次相关分析。
-
模型算法情况?
-
SPSSAU20.0提供的的个体固定和个体随机效应模型,当前版本暂未提供时间固定或时间随机效应模型。
-
时间固定和双向固定什么意思?
-
通常情况下,面板模型仅考虑个体固定模型(SPSSAU默认提供的FE模型)。如果说希望考虑时间效应,可选中‘时间固定’复选框。针对时间固定效应的检验上,建议可先使用‘计量研究’->‘OLS回归’,将时间作为虚拟哑变量纳入模型中,如果时间项基本均呈现出显著性,说明可以考虑时间效应。反之如果时间项基本没有呈现出显著性,那么可不考虑时间效应(面板模型分析时,绝大多数情况下均不应该考虑时间效应)。
-
如果说需要同时考虑时间效应和个体效应,那么可选中‘双向固定’复选框。
-
SPSSAU面板模型中的robust法?
-
SPSSAU进行面板模型时,robust参数复选框,默认为‘稳健聚类robust法’,该方法可在一定程度上处理异方差问题。
-
SPSSAU进行面板模型提示‘数据格式不对’?
-
如果使用SPSSAU中出现数据格式不对的提示,可查看研究方法数据格式说明,请点击查看。
-
面板数据提示‘数据格式不对’如何检查?
-
如果出现‘数据格式不对’的提示,建议可使用通用方法模块中的’分类汇总’功能进行查看,操作类似如下:
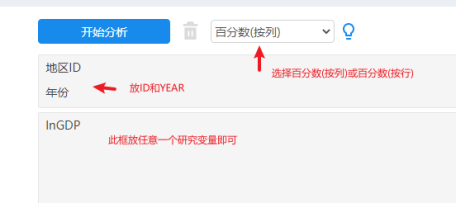
-
面板数据的格式上,1个id在1个年份上,肯定只会有1个数字。如果发现结果中某个id在某年上出现数字大于1,那么数据格式肯定不正确,建议修正后再次查看。更多数据格式可点击查看。
-
面板模型时R 方值小于0?
-
从数据原理上,面板模型的R 方值可小于0,通常情况下面板模型对R 方值关注较低,建议忽略即可。
-
面板模型时希望输出各id项的回归系数?
-
SPSSAU进行面板模型分析时,如果希望输出各个id项的回归系数,此时需要使用LSDV法得到,具体操作如下说明:
-
1、将id项作哑变量处理,比如有100个id项,即得到100个哑变量;
-
2、将任意1个哑变量(通常是第1个)作为参照项,余下99个哑变量放入模型中;
-
3、参照项的回归系数=0-其余99个回归系数之和;
-
4、查看POOL模型里面的结果,即得到具体id项的回归系数信息等。 更多关于哑变量说明,可点击查看。
-
面板模型Hausman检验原理?
-
在进行Hausman检验时,其自由度为X个数,但当某X无法计算出标准误时,此时该项则不计入自由度中,此算法于2022.11.24号进行升级。
-
面板模型时如果R 方出现为负数时的处理?
-
在面板模型时,原理上R 方可以为负数,当出现时影响作用关系的数据依旧可使用,但R 方值无意义建议此时忽略该指标即可。
-
SPSSAU进行面板模型时输出面板单位根检验LLC和IPS?
-
如果选中‘LLC检验和IPS’检验,则SPSSAU会进行面板单位根检验,默认仅针对被解释变量进行,当然也可针对被解释变量和解释变量均进行面板单位根检验。另系统会进行自动判断,如果是平衡面板数据则会输出LLC检验和IPS检验两项,如果是非平衡面板数据此时只会输出IPS检验。通常情况下IPS检验的适用范围更广泛尤其对异质性较强的数据时,并且IPS检验适用于平衡和非平衡面板数据,以及LLC检验对于长面板数据可能更适合以及其只针对平衡面板数据。
