-
OLS回归(社会学研究称为线性回归),也称作最小二乘法回归。在计量经济学研究中,一般称之为OLS回归。OLS回归研究X对于Y的影响,在计量研究中,异方差问题非常重要,严重的异方差问题会影响模型估计和模型检验等,因而在OLS回归时需要对其进行检验,如果出现异方差问题则需要进行处理等。
关于异方差的检验上,SPSSAU提供两种检验方法,分别是怀特(White)异方差检验和BP检验,通常情况下我们使用怀特(White)异方差检验即可。另外,处理异方差问题有三种办法,分别是数据处理、稳健标准误回归、FGLS回归(可行广义最小二乘法回归)。分别如下:
-
针对连续且大于0的原始自变量X和因变量Y,进行取自然对数(或10为底对数)操作,如果是定类数据则不处理。取对数可以将原始数据的大小进行‘压缩’,这样会减少异方差问题。事实上多数研究时默认就进行此步骤处理,而不需要先异方差检验发现有异方差再进行处理。负数不能直接取对数,如果数据中有负数,研究人员可考虑先对小于0的负数,先取其绝对值再求对数,然后加上负数符号。
-
如果检验显示有异方差问题,可使用Robust稳健标准误回归法进行研究。此种研究方法是当前最为流行也最为有效的处理办法。
-
如果发现有异方差问题,还可使用FGLS法进行分析,以处理异方差问题。FGLS是这样的一类思路,即对于残差值越大的点,给予越小的权重,从而解决异方差问题,FGLS回归事实上一系列数据处理的过程,并且它是一种思路。从分析上看,它依然还是使用OLS回归方法进行,具体在案例里面会详细讲解。
数据处理
Robust稳健标准误回归
FGLS回归
-
OLS回归案例
-
1、背景
当前进行一项雇员工资影响因素研究,影响因素X共有四项,分别是‘起始工资’,性别,受雇月数和受教育年限。因变量Y为当前工资。如下表:
变量 名称 自然对数ln处理 因变量Y 当前工资 需要 自变量X1 起始工资 需要 自变量X2 性别 不需要 自变量X3 受雇月数 需要 自变量X4 受教育年限 需要 上表格中‘当前工资’,‘起始工资’,‘受雇月数’和‘受教育年限’共四项,它们均为连续数据而且数字全部大于0,因此可直接取对数(自然对数)处理,以减少异方差问题。
-
2、理论
OLS回归研究X对于Y的影响,在计量研究中,需要将异方差问题考虑在内,异方差问题可使用怀特(White)异方差检验和BP检验进行检验【SPSSAU默认提供】,如果出现异方差问题,可使用Robust稳健标准误回归、FGLS可行性广义最小二乘法回归进行异方差处理等。
-
特别提示
-
如果进行Robust稳健标准误回归,则不会继续输出怀特(White)异方差检验和BP检验,研究人员可直接以Robust稳健标准误回归作为最终结果;Robust稳健标准误回归是一种非常有效的异方差处理方式,有时候研究人员默认使用Robust稳健标准误回归进行研究,不论是否出现异方差检验不通过的现象;
-
-
3、操作
本例子研究‘起始工资,性别,受雇月数和受教育年限’共四项对于当前工资的影响关系,研究数据共为200份。操作如下图所示:
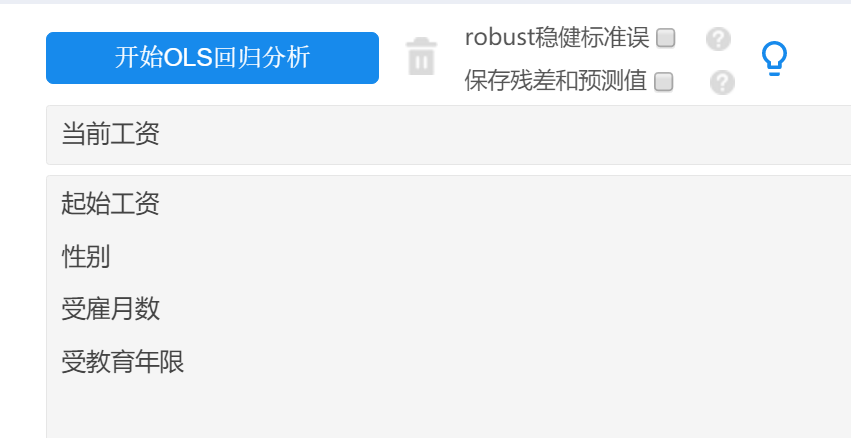
默认操作时没有进行取自然对数操作,输出异方差结果如下表格:
异方差检验结果 White 异方差检验 BP 异方差检验 χ2 p χ2 p 43.530 0.000 37.631 0.000 使用怀特(White)检验和BP检验两种方法进行检验。检验原假设为模型没有异方差,上表显示两种检验均拒绝原假设(p < 0.05),说明模型确实存在异方差,当存在异方差问题时,共有三种处理方式,一是对数据取对数,二是使用Robust稳健标准误回归,三是使用FGLS回归。当然也可以同时进行,比如取对数和使用Robust稳健标准误回归;也或者取对数,Robust稳健标准误回归和FGLS回归同时进行。
如果是使用取对数和Robust稳健标准误回归,则先对数据取对数(使用数据处理->生成变量功能),然后进行SPSSAU操作如下:
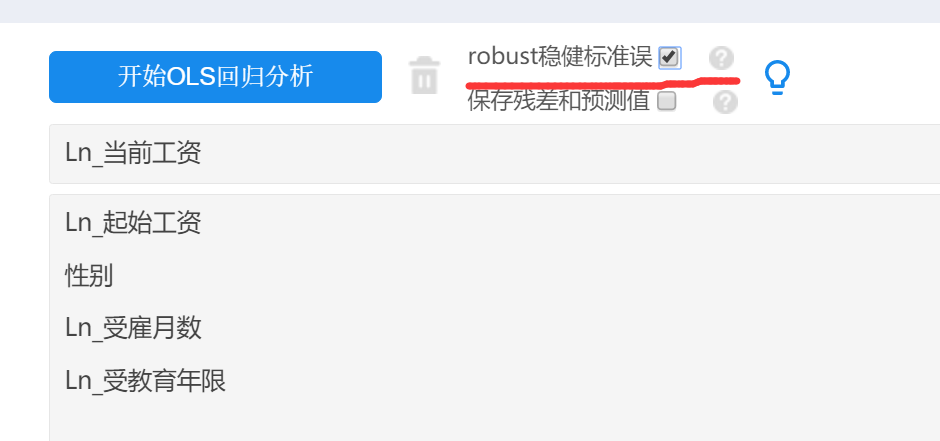
除此之外,还可以使用FGLS法进行异方差处理,FGLS法进行异方差处理共分为4个步骤,分别如下:
-
Step1:进行OLS回归(因变量为,并且选择‘保存残差和预测值’,得到残差值residual,操作如下图:
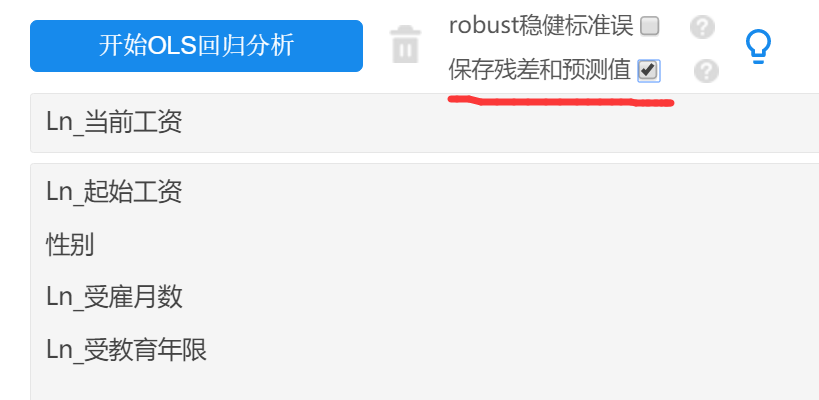
-
Step2:计算残差值的平方residual^2,然后取对数ln(residual^2);此处理使用SPSSAU的生成变量即可完成;如下图:
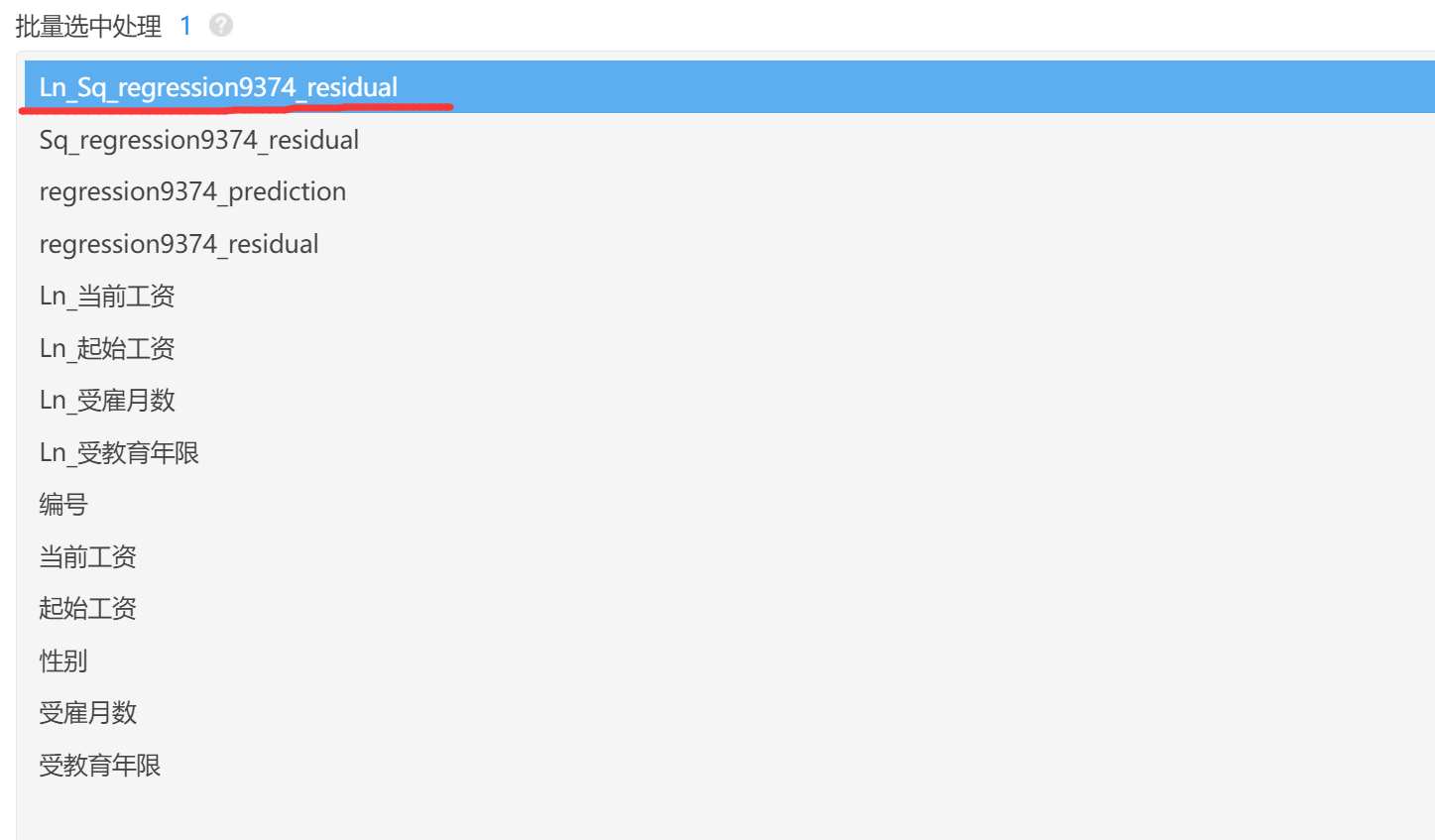
-
特别提示
-
由于残差值很可能小于0,所以取其平方,然后再取自然对数。
-
Step3:将上一步得到的ln(residual^2),作为因变量Y,自变量和Step1一致,进行OLS回归,并且选择‘保存残差和预测值’,得到预测值prediction;
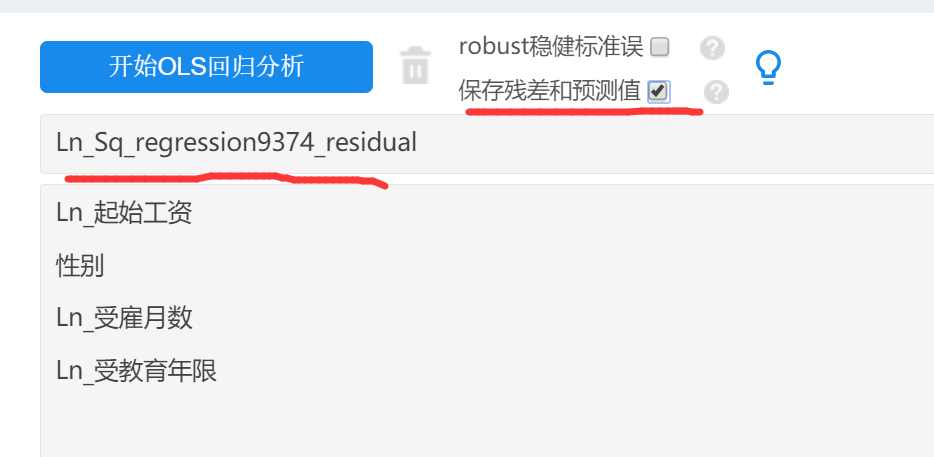
-
Step4:将Step3得到的预测值取指数幂,即e^prediction。然后再取倒数,最终得到为1 / e^prediction【特别提示:SPSSAU暂没有提供指数幂功能,可在EXCEL中完成即可】。
-
Step5:将Step4得到的数据1 / e^prediction作为加权项进行OLS回归,如下图操作:

上述5个步骤即为FGLS法,FGLS法是一系列操作步骤,其实质依旧是OLS回归。
-
-
4、SPSSAU输出结果
针对上述例子,输出为上述使用FGLS法的结果,如下所示:
异方差检验结果 White 异方差检验 BP 异方差检验 χ2 p χ2 p 12.620 0.478 4.489 0.344 使用FGLS法后依然可以进行异方差检验,上表格显示怀特(White)检验和BP检验两种方法均显示没有异方差问题。有时候会出现white检验和BP检验的结论不一致,如果出现此类情况,建议使用White检验作为最终结论。
另外,FGLS法事实上就是处理异方差问题的解决方法,而FGLS法后依旧可以出现异方差检验的结果,但事实上FGLS法已经是最终结点,即使FGLS法后还显示异方差也不需要继续过多考虑,否则会无穷无尽死循环。
OLS回归分析结果-简化格式 值 常数 -3.220
(-2.572*)Ln_起始工资 0.916
(17.815**)性别 0.024
(0.861)Ln_受雇月数 0.922
(3.722**)Ln_受教育年限 0.228
(3.389**)R 2 0.797 调整R 2 0.793 F 值 191.156(0.000**) 因变量(Y):Ln_当前工资 D-W值:1.825 * p < 0.05 ** p < 0.01 括号里面为t 值 -
5、文字分析
OLS回归分析结果-简化格式 值 常数 -3.220
(-2.572*)Ln_起始工资 0.916
(17.815**)性别 0.024
(0.861)Ln_受雇月数 0.922
(3.722**)Ln_受教育年限 0.228
(3.389**)R 2 0.797 调整R 2 0.793 F 值 191.156(0.000**) 因变量(Y):Ln_当前工资 D-W值:1.825 * p < 0.05 ** p < 0.01 括号里面为t 值 本次研究‘起始工资,性别,受雇月数和受教育年限’共四项对于当前工资的影响关系,研究数据共为200份。第一次进行OLS回归,即直接将‘起始工资,性别,受雇月数和受教育年限’共四项放入模型时发现,数据具有异方差问题。因此对起始工资,受雇月数,受教育年限共三项取自然对数处理,并且使用FGLS可行性最小二乘法进行异方差问题处理,最终结果如上表所示:
上表显示,模型R 2值为0.797,意味着‘起始工资,性别,受雇月数和受教育年限’共四项可以解释当前工资79.7%的变化原因,而且模型通过F 检验,意味着模型有意义。
具体分析来看,起始工资的回归系数值为0.916,并且呈现出0.01水平显著性(t =17.815,p =0.000 < 0.01),说明起始工资对于当前工资表现出显著的正向影响关系,起始工资每增加一个单位时,当前工资会增加0.916个单位。以及性别的回归系数值为0.024,但是并没有呈现出显著性( t =0.861,p =0.390> 0.05),意味着性别对当前工资水平没有影响关系。受雇月数的回归系数值为0.922,并且呈现出0.01水平显著性(t =3.722,p =0.000 < 0.01),意味着受雇月数会对当前工资产生显著的正向影响关系,受雇佣时间越长工资水平也会越高。受教育年限的回归系数值为0.228,并且呈现出0.01水平显著性( t =3.389,p =0.001< 0.01),意味着受教育年限会对当前工资产生显著的正向影响关系,受教育年限越多时,当前工资水平也会越高。
-
6、剖析
涉及以下几个关键点,分别如下:
-
有时候会出现white检验和BP检验的结论不一致,如果出现此类情况,建议使用White检验作为最终结论;
-
解决异方差问题一般有三种办法,分别是数据处理(取对数)、Robust稳健标准误回归和FGLS法;三种办法可以同时使用去解决异方差问题;
-
如果是取对数操作,特别需要注意原始数据中负数不能直接取对数,如果数据中有负数,研究人员可考虑先对小于0的负数,先取其绝对值再求对数,然后加上负数符号;
-
Robuust稳健标准误回归不会输出white检验和BP检验,Robust稳健标准误回归即是最终结果;
-
FGLS法事实上就是处理异方差问题的解决方法,而FGLS法后依旧可以出现异方差检验的结果,但事实上FGLS法已经是最终结点,即使FGLS法后还显示异方差也不需要继续过多考虑,否则会无穷无尽死循环。
-
疑难解惑
-
F 值括号里面的两个值分别是什么?
-
如果是F 值想计算得到p 值,需要提供两个自由度值df 1和df 2。一般情况下,df 1等于自变量数量;df 2等于样本量 - (自变量数量+1)。此两个值仅为中间过程值,规范格式上需要写成这样而已,无其它实际意义。
-
SPSSAU OLS回归时没有输出white或bp检验?
-
如果说选中了‘robust稳健标准误’,此时ols回归则不会输出white和bp检验,将robust稳健标准误不选中就好。
-
AIC值和BIC值计算说明?
-
SPSSAU中OLS模型时,输出AIC和BIC值均进行过样本量惩罚项处理,因此完全相同模型前提下时,其与通用方法里面的线性回归输出的AIC和BIC指标值不同。
-
OLS回归进行遗漏变量检验Ramsey rest test?
-
SPSSAU默认提供遗漏变量检验Ramsey rest test,如果考虑遗漏变量问题时则需要查看该检验(反之不需要),以及遗漏变量检验Ramsey rest test时很容易出现严重共线性,出现此情况下SPSSAU会进行提示检验结论可能不可靠,此时建议谨慎使用。
-
OLS回归时放入定类项如何分析?
-
OLS回归中自变量X支持放入为定类项,此时SPSSAU会自动对定类项进行虚拟(哑)变量处理,并且进行分析,哑变量处理后默认以第1项作为参照项。具体关于虚拟(哑)变量的理论知识和说明,可点击查看。
