-
逐步回归分析研究X(自变量,通常为量数据)对Y(因变量,定量数据)的影响关系情况,X可以为多个,但并非所有X均会对Y产生影响;当X个数很多时,可以让系统自动识别出有影响的X;这一自动识别分析方法则称为逐步回归分析;如果全部X均没有显著性,此时系统默认返回 回归分析结果。
-
-
分析步骤共为四步,分别是:
-
第一步:首先对模型情况进行分析
-
首先分析最终余下的X情况;以及被模型自动排除在外的X; 接着对模型拟合情况(比如R 2为0.3,则说明所有余下X可以解释Y 30%的变化原因),模型共线性问题(VIF值小于5则说明无多重共线性).
-
第二步:分析X的显著性
-
模型余下的X一定具有显著性;具体分析X的影响关系情况即可.
-
第三步:判断X对Y的影响关系方向
-
回归系数B值大于0说明正向影响,反之负向影响.
-
第四步:其它
-
比如对比影响程度大小(回归系数B值大小对比X对Y的影响程度大小)..
分析项 逐步回归分析说明 网购满意度,重复购买意愿 网购满意度20项;其中具体那几项会影响到样本重复购买意愿?20项过多,让软件自动删除掉没有影响的项,余下有影响的项 -
-
分析结果表格示例如下:
非标准化系数 标准化系数 t p VIF R 2 调整R 2 F B 标准误 Beta 常数 0.774 0.384 - 2.014 0.047* - 0.351 0.326 14.188** 分析项1 0.198 0.099 0.202 1.998 0.048* 1.320 分析项2 0.437 0.124 0.374 3.519 0.001** 1.320 分析项3 0.004 0.124 0.004 0.034 0.973 1.230 * p <0.05 ** p <0.01 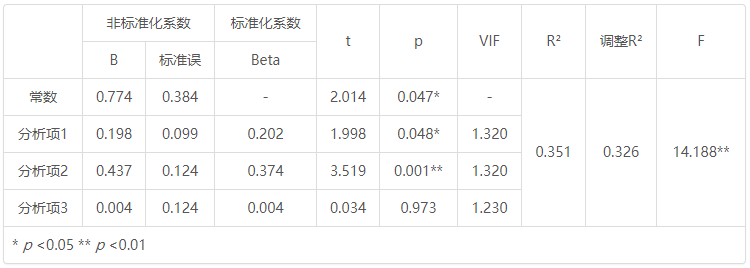
-
特别提示
-
逐步回归分析仅在回归分析的基础上,加入了一项功能,即自动化移除掉不显著的X,通常逐步回归分析用于探索研究中。
-
逐步回归分析之后,可对回归模型进行检验。可包括以下四项:
-
多重共线性:可查看VIF值,如果全部小于10(严格是5),则说明模型没有多重共线性问题,模型构建良好;反之若VIF大于10说明模型构建较差。
-
自相关性:如果D-W值在2附近(1.7~2.3之间),则说明没有自相关性,模型构建良好,反之若D-W值明显偏离2,则说明具有自相关性,模型构建较差。自相关问题产生时建议对因变量Y数据进行查看。
-
残差正态性:在分析时可保存残差项,然后使用“直方图”直观检测残差正态性情况,如果残差直观上满足正态性,说明模型构建较好,反之说明模型构建较差。如果残差正态性非常糟糕,建议重新构建模型,比如对Y取对数后再次构建模型等。
-
异方差性:可将保存的残差项,分别与模型的自变量X或者因变量Y,作散点图,查看散点是否有明显的规律性,比如自变量X值越大,残差项越大/越小,这时此说明有规律性,模型具有异方差性,模型构建较差。如果有明显的异方差性,建议重新构建模型,比如对Y取对数后再次构建模型等。
-
另外,如果回归分析出现各类异常,请查看数据中是否有异常值(可通过比如描述分析、箱线图、散点图等查看),找出异常值,并且处理掉异常值(使用“异常值”功能)。也或者使用稳健回归(Robust回归进行分析,Robust回归是专门处理异常值情况下的回归模型)。
-
-
SPSSAU操作截图如下:
-
疑难解惑
-
提示“模型没有识别出显著自变量!”?
-
逐步回归可自动识别出对因变量有影响的自变量X,当然有可能所有的自变量均不会对因变量产生影响,则会出现此提示。可使用‘线性回归’进行对比检查。
-
F 值括号里面的两个值分别是什么?
-
如果是F 值想计算得到p 值,需要提供两个自由度值df 1和df 2。一般情况下,df 1等于自变量数量;df 2等于样本量 - (自变量数量+1)。此两个值仅为中间过程值,规范格式上需要写成这样而已,无其它实际意义。
-
常数项值很大或者很小?
-
常数项无实际意义,包括其对应的显著性值等均无实际意义,只是数学角度上一定存在而已。
-
自变量进入或者移出模型的标准?
-
SPSSAU进行逐步回归时,使用p 值作为自变量进入或者移出模型作为标准(与IBM SPSS软件保持一致),具体进入模型标准为p 值小于0.05,移出模型标准为p 值大于0.1。【此算法于20220317日进行过更新,旧版本使用F值大于3.84作为进入标准,F值小于2.71作为移出标准】
-
逐步回归的三种方法逐步法、向前法和向后法?
-
SPSSAU进行逐步回归时共提供3种方式,默认为逐步stepwise法,可选为向前forward法和向后backward法。一般情况下使用Stepwise法最多。
-
SPSSAU逐步回归之后还是出现p >0.05?
-
逐步回归的原理上可能出现此种情况,即最终留在模型里面的某个X对应p 值依旧大于0.05,这是由数学原理决定。如果对该结果不认可,建议可‘主观’式移除不显著项,然后进行线性回归分析即可。
