-
主成分分析用于对数据信息进行浓缩,比如总共有20个指标值,是否可以将此20项浓缩成4个概括性指标。除此之外,主成分分析可用于权重计算和综合竞争力研究。即主成分分共有三个实际应用场景:
-
-
信息浓缩:将多个分析项浓缩成几个关键概括性指标;
-
权重计算:利用方差解释率值计算各概括性指标的权重;
-
综合竞争力:利用成分得分和方差解释率这两项指标,计算得到综合得分,用于综合竞争力对比(综合得分值越高意味着竞争力越强)。
主成分(pca)分析通常有三个步骤;第一步是判断是否适合进行主成分(pca)分析;第二步是主成分与分析项对应关系;第三步是主成分命名.
-
第一步:判断是否进行主成分(pca)分析;判断标准为KMO值大于0.6.
-
第二步:主成分与分析项对应关系判断.
-
特别提示:如果研究目的完全在于信息浓缩,并且找出主成分与分析项对应关系,此时SPSSAU建议使用因子分析【请参考因子分析手册】,而非主成分分析。主成分分析目的在于信息浓缩(但不太关注主成分与分析项对应关系),权重计算,以及综合得分计算。
-
特别提示:有时不太会关注主成分与分析项的对应关系情况,比如进行综合竞争力计算时,不需要过多关注主成分与分析项的对应关系情况。
-
主成与分析项对应关系判断:假设预期为3个主成分,分析项为10个;主成分与分析项交叉共得到30个数字,此数字称作“载荷系数”(载荷系数值表示分析项与主成分之间的相关程度); 针对每个主成分,对应10个”载荷系数”,针对每个分析项,则有3个“载荷系数值”(比如0.765,-0.066,0.093),选出3个数字绝对值大于0.4的那个值(0.765),如果其对应主成分1,则说明此分析项应该划分在主成分1下面.
-
对不合理分析项进行删除,共有三种情况; 第一类:如果分析项的共同度(公因子方差)值小于0.4,则对应分析项应该作删除处理;第二类:某分析项对应的“载荷系数”的绝对值,全部均小于0.4,也需要删除此分析项;第三类:如果某分析项与主成分对应关系出现严重偏差(通常也称作‘张冠李戴’),也需要对该分析项进行删除处理.
-
第三步:主成分命名
-
在第二步删除掉不合理分析项后,并且确认主成分与分析项对应关系良好后,则可结合主成分与分析项对应关系,对主成分进行命名.
-
-
分析结果表格示例如下(SPSSAU同时会生成碎石图):
载荷系数 共同度(公因子方差) 主成分1 主成分2 主成分3 分析项1 0.765 -0.066 0.093 0.598 分析项2 0.676 0.081 -0.017 0.464 分析项3 0.657 0.207 -0.205 0.517 分析项4 0.645 0.271 0.089 0.497 分析项5 0.501 0.457 0.085 0.467 分析项6 0.311 0.697 -0.005 0.583 分析项7 0.226 -0.669 0.130 0.516 分析项8 0.191 0.644 0.046 0.453 分析项9 0.476 -0.187 0.542 0.555 分析项10 0.001 -0.048 0.968 0.939 -
特别提示
-
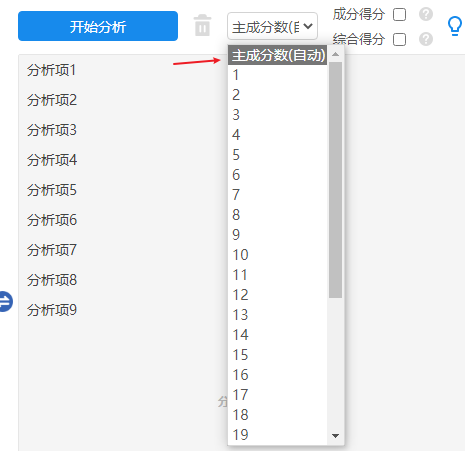
主成分(pca)分析进行信息浓缩时,可能会经历多次重复循环,删除不合理项,并且重复多次循环,最终得到合理结果。
SPSSAU操作截图如下:
-
-
-
特别提示
-
关于“保存成分得分”:主成分(pca)分析将信息浓缩成几个主成分,并且可让系统保存“成分得分”。成分得分可用于进一步分析,比如聚类分析,回归分析使用等。
-
关于“保存综合得分”:如果使用主成分(pca)分析的目的在于进行综合竞争力排名,比如银行的绩效排名,上市公司竞争力排名等,此时可直接保存综合得分,用于竞争力排名。
-
-
主成分(pca)分析说明
本部分针对主成分的三种应用场景进行说明,包括信息浓缩,权重计算,和综合竞争力计算。
-
1、信息浓缩
关于信息浓缩,即将多个分析项信息浓缩成几个概括性指标,而且希望进行主成分命名,SPSSAU建议使用因子分析。原因在于因子分析在主成分基础上,多出一项旋转功能,该旋转目的即在于命名。
如果研究目的更多在于将多个指标进行浓缩成几个概括性指标,此时直接使用因子分析更优。实际研究中,主成分目的更多在于权重计算和综合得分计算(当然这两项功能在因子分析中也有)。
-
2、权重计算
权重计算是主成分的一类应用场景,其原理在于使用方差解释率进行权重计算,方差解释率是指概括性指标(即主成分),对应提取的信息量。如下表详细讲述:
方差解释率表格 编号 特征根 主成分提取 特征根 方差解释率% 累积% 特征根 方差解释率% 累积% 1 5.856 58.563 58.563 5.856 58.563 58.563 2 0.999 9.988 68.551 0.999 9.988 68.551 3 0.656 6.558 75.109 0.656 6.558 75.109 4 0.584 5.839 80.948 - - - 5 0.507 5.07 86.018 - - - 6 0.382 3.816 89.833 - - - 7 0.341 3.409 93.243 - - - 8 0.269 2.689 95.932 - - - 9 0.227 2.271 98.203 - - - 10 0.18 1.797 100 - - - -
上表格显示:共10个分析项进行分析,最终提取得到三个主成分【主成分数量可自行设置】,此3个主成分方差解释率分别是58.563%,9.988%,6.558%,累积方差解释率为75.109%。即说明三个主成分,分别提取出共10项的信息量分别是58.563%,9.988%和6.558%,累积三个主成分表达10个分析项共计75.109%的信息量。通常情况下,权重加和均为100%,但这里为75.109%,此时即需要进行加权处理,即默认理解三个主成分完全表达10个分析项。加权处理方法为:方差解释率 除 累积方差解释率。
-
本例子,三个主成分对应的加权后方差解释率即权重依次为:58.563/75.109=77.97%;9.988/75.109=13.30%;6.558/75.109=8.73%。即如果是计算权重,三个主成分的权重分别是77.97%,13.30%和8.73%。
-
-
3、 综合得分【综合竞争力】
主成分分析还有一类非常重要的应用场景即计算综合得分,利用综合得分去对比综合竞争力情况,综合得分值越高,此时综合竞争力越强。此类应用常见于经济、管理类研究,比如上市公司的竞争实力对比。
综合得分是利用“成分得分系数矩阵”,以及方差解释率进行进一步计算而得到。
-
“成分得分系数矩阵”可用于计算每个成分得分;
-
每个成分得分计算后,结合方差解释率,最终即得到综合得分。【方差解释率越高,说明该主成分越重要,权重占比也应该越高】详细说明如下:
成分得分系数矩阵 名称 成分 成分1 成分2 成分3 成分4 成本收入比 0.888 -0.085 0.123 0.108 不良贷款比例 0.763 0.325 0.231 -0.051 人均利润率 0.718 0.124 0.181 0.539 总资产净利率ROA -0.265 0.851 0.312 0.068 净资产收益率ROE 0.135 0.689 -0.033 -0.648 资本充足率 -0.498 0.152 0.685 0.331 存贷比 0.327 0.419 -0.621 0.229 存款增长率 0.487 -0.393 0.443 -0.510 -
上表格中显示共有四个主成分,四个主成分分别与分析项的关系表达式如下:
-
主成分1得分=0.888*成本收入比+0.763*不良贷款比例+...+0.487*存款增长率
-
主成分2得分=-0.085*成本收入比+0.325*不良贷款比例+...-0.393*存款增长率
-
主成分3得分=0.123*成本收入比+0.231*不良贷款比例+...+0.443*存款增长率
-
主成分4得分=0.108*成本收入比-0.051*不良贷款比例+...-0.510*存款增长率
-
利用上述表达式,可计算出四个主成分得分【SPSSAU可输出】。
-
接着计算综合得分【SPSSAU可输出】;综合得分需要结合主成分分别对应的方差解释率相乘后加和,并除以累积方差解释率,计算公式如下:综合得分=(w1*主成分1得分+w2*主成分2得分+w3*主成分3得分+w4*主成分4得分)/ 累积方差解释率, w1,w2,w3和w4分别表示四个主成分的方差解释率。综合得分计算完成后,其分值越大,则说明竞争力越强。
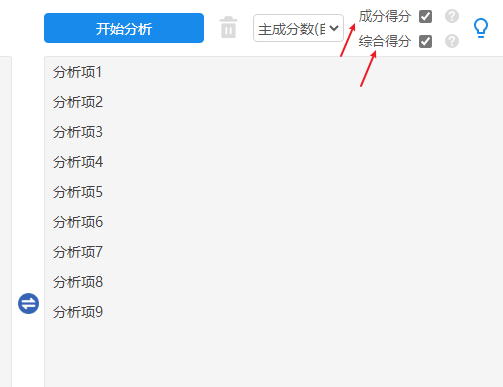
SPSSAU可输出主成分得分和综合得分,操作如下图:
-
疑难解惑
-
成分得分后用于回归分析?
-
主成分得分可用于进一步分析使用如果进行回归分析(这种方式叫主成分回归),成分得分需要选中按钮才会生效,且SPSSAU单独生成新标题名称类似为:“PCA****_score1”。用户可通过【数据处理->标题处理】对名称进行修改即可。

-
综合得分如何使用?
-
综合得分可用于对比综合竞争力情况,综合得分值越高,此时综合竞争力越强。此类应用常见于经济、管理类研究,比如上市公司的竞争实力对比。
-
综合得分需要选中按钮才会生效,且SPSSAU单独生成一列新标题名称类似为:“Comp_score****”,一般情况下用户需要把综合得分的原始数据下载出来使用,通过右上角‘我的数据->下载’,可将综合得分下载出来使用。
-
提示出现奇异矩阵?
-
如果提示出现“奇异矩阵”,通常情况下由于分析样本量太少(比如分析项有20个,分析样本仅10个),此里需要加大样本量或者减少分析项即可;以及还有一种情况是分析项之间的相关性非常非常弱或者非常非常强,此时需要移除掉相关性非常弱或者非常强的分析项(使用相关分析进行检查相关关系)。
-
‘分析之前是否需要对数据进行标准化处理’?
-
SPSSAU默认就已经进行过标准化处理,因此不需要再对数据处理。当然标准化后的数据再次标准化依旧还是自身没有任何变化,结果永远均一致。
-
综合得分如何计算得到的?
-
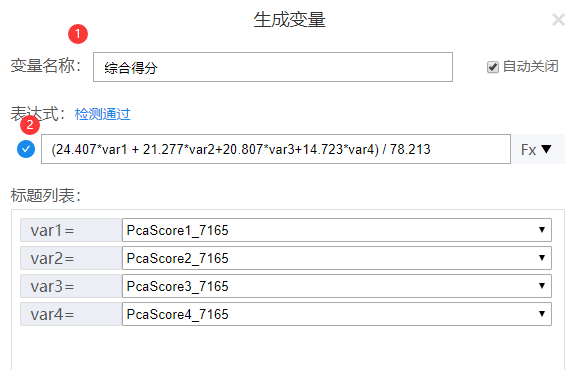
SPSSAU默认提供保存综合得分,至于其计算原理,比如说提取得到4个主成分,并且此4个主成分的方差解释率分别是21.407%,21.277%,20.807%和14.723%;累积方差解释率值为78.213%。综合得分计算公式为:求和(主成分得分*方差解释率)/累积方差解释率。如下图所示:
-
综合得分如何使用?
-
SPSSAU默认可保存综合得分(以及因子得分等);一般该值越大表示越有竞争力等;研究者通常需要把综合得分的具体数据下载后使用,并且在EXCEL进行排序(也可使用SPSSAU生成变量里面的排序功能)。 通过右上角我的数据可下载具体综合得分的具体数据等。
-
特征根值没有大于1可以吗?
-
主成分分析时通常需要综合自己的专业知识,以及软件结果进行综合判断,即使是特征根值小于1,也一样可以提取主成分。
-
载荷图?
-
载荷图是针对成分与旋转后载荷值关系的图形化展示,使用较少,通常需要手工加‘圆圈’把挨在一起的因子圈起来,更直观展示成分与分析项的隶属对应关系情况。由于可读性和解释性问题,一般只关注于方差解释率靠前的前面几个成分,多数情况下只关注2个。
-
主成分回归是什么意思?
-
进行主成分时,选择保存‘成分得分’,然后利用系统生成的‘成分得分’数据进行线性回归,即为主成分回归。
-
为什么没有出现‘成份得分系数矩阵’,成分得分,综合得分?
-
如果说主成分分析计算过程中出现无法计算成成份得分(通常是内部算法出现矩阵不可逆),此时默认不输出‘成份得分系数矩阵’,同时如果选中成分得分或综合得分,此两项也无法计算,因此也不进行输出。
-
累积方差解释率出现100%以上如何办?
-
正常情况下,累积方差解释率会小于100%,但如果数据的共线性问题太严重,有可能出现方差解释率值大于100%,此时建议进行相关分析,找出相关性太强(比如相关系数大于0.8)的项,然后从分析框中移出后再次分析。与此同时,如果样本量太少也可能出现此问题建议加大样本量即可。
-
主成分分析时,KMO值为null不存在?
-
原理上主成分分析要求各个分析项之间有着适中的相关关系(不能过高或过低)。如果分析项之间的相关系数值过高(比如大于0.8),说明共线性太强,无法有效浓缩信息,此种情况可能导致KMO值无法输出。建议在进行因子分析前可先进行相关分析进行查看各分析项间的相关系数情况,移除掉相关系数值过高项之后,再次进行分析即可。
-
样本量过少容易导致相关系数过高,一般希望分析样本量大于5倍分析项个数。
-
提示:KMO值综合衡量分析项间的信息重叠情况(即分析项之间的相关关系情况)。分析项之间的相关系数过低(比如小于0.2或没有显著性),信息重叠度低无法有效浓缩信息,这会导致KMO值较低,如果分析项之间的相关系数过高(比如大于0.8),这会导致严重共线性可能无法输出KMO值。分析项之间的相关系数值一般希望介于0.3~0.7之间较好。
-
解决办法
-
先检查相关关系情况,并且移除掉相关系数过高项后再次分析;
-
加大样本量,建议分析样本量大于5倍分析项个数。
-
KMO值过低?
-
一般需要KMO值大于0.6即可,如果是两个分析项,KMO值一定是0.5;因而建议删除掉共同度(公因子方差)值较低项,这样可以提升KMO值。
-
如果不输出KMO值,意味着数据质量过差,建议可使用相关分析看下相关关系,如果相关系数值基本均小于0.3(或者没有呈现出显著性),则说明题项间关联性弱,则KMO值一定会较低,建议先移除相关系数值较低项后再次分析。
-
提示:KMO值综合衡量分析项间的信息重叠情况(即分析项之间的相关关系情况)。分析项之间的相关系数过低(比如小于0.2或没有显著性),信息重叠度低无法有效浓缩信息,这会导致KMO值较低,如果分析项之间的相关系数过高(比如大于0.8),这会导致严重共线性可能无法输出KMO值。分析项之间的相关系数值一般希望介于0.3~0.7之间较好。
-
主成分回归是什么意思?
-
主成分分析后,选中保存‘成分得分’,SPSSAU系统会新生成标题用于标识‘成分得分’,比如:PcaScore1_1234,继续使用‘成分得分’用于接下来的线性回归分析,即称作‘主成分回归’,通常‘主成分回归’用于解决共线性问题。
-
指标计算权重?
-
主成分分析的原理在于信息浓缩,对于信息浓缩的帮助越大,指标权重可越大,正是利用此原理,可进行指标权重的计算。信息浓缩的帮助情况使用载荷系数值进行表示。在计算指标权重时,共分为3步:
-
第1步:计算线性组合系数,其公式为:loading矩阵/Sqrt(eigen),即载荷系数除以对应特征根的平方根。可以看出,线性组合系数可用于表述了信息浓缩的大小;
-
第2步:计算综合得分系数,公式为:累积(线性组合系数*方差解释率)/累积方差解释率,即线性组合系数分别与方差解释率相乘后累加,然后除以累积方差解释率;
-
第3步:计算权重,将综合得分系数进行归一化处理即得到各指标权重值;
-
特别说明:从数学角度上有可能得到的权重值为负数,如果出现负数,SPSSAU会自动对loading绝对值然后再进行权重计算。
-
SPSSAU时,面板数据如何进行主成分分析?
-
面板数据可直接进行主成分分析,面板数据格式相对较为特殊,在分析上直接针对研究指标进行分析即可,数据格式可点击查看。
-
SPSSAU时,成分得分是标准化后的数据进行吗?
-
成分得分的数据计算,默认是基于标准化后的数据进行。
-
SPSSAU输出MSA指标?
-
进行因子分析或主成分析时,选择‘相关系数矩阵’时,SPSSAU则会输出MSA指标和相关系数矩阵信息等,其用于分析研究项是否适合进行因子分析,如果MSA指标值过低时,可考虑将该类项从模型中移出去。
-
保存因子得分或综合得分,但并没有保存?
-
在主成分分析或者因子分析时,如果选中保存因子得分(或者综合得分),但分析后标题框中未出现新的标题来标识,原因在于在计算因子得分(或综合得分)时,出现矩阵不可逆无法计算,因而无法保存。研究者应该使用共线性分析,检查数据是否存在严重的共线性问题(特征是相关系数基本接近于1或者-1),以及累积方差解释率会出现两个(甚至多个)为100%甚至高于100%的情况。将共线性严重的项移除出去不分析再做分析即可正常得到。
