-
分层回归的核心即为回归分析;区别在于分层回归可分为多层;比如第一次放入4个X;第二层放入3个X;第3层放入2个X; 每一层均在上一层基础上放入更多项;那放入的更多项是否对模型有解释力度,此则为分层回归关心的问题;分层回归通常用于中介作用或者调节作用研究中。
-
-
分析步骤共为四步,分别是:
-
第一步:首先对模型情况进行分析分析描述各个模型的拟合情况,以及R 2值的变化情况.
-
第二步:分析X的显著性结合自身需要;分析具体X的显著性情况.
-
第三步:判断X对Y的影响关系方向回归系数B值大于0说明正向影响,反之负向影响.
-
第四步:其它结合不同模型的对比,得出相关结论(比如中介作用或者调节作用研究的相关结论).
分析项 分层回归分析说明 网购满意度,重复购买意愿 第一层放入性别,学历,年龄,收入等基本个人信息; 第二层放入核心研究项; 深入说明核心研究项对于重复购买意愿的影响情况?(核心研究项加入后,R 2有明显变化) -
-
分析结果表格示例如下:
分层1 分层2 B 标准误 t p B 标准误 t p 常数 10.722** 1.493 7.179 0 12.069** 1.682 7.178 0 分析项1 0.207 0.409 0.507 0.612 0.354 0.423 0.837 0.404 分析项2 -0.047 0.41 -0.113 0.91 0.164 0.435 0.376 0.707 分析项3 -0.44 0.373 -1.178 0.24 分析项4 -0.09 0.067 -1.343 0.181 R 2 0.001 0.017 调整R 2 -0.009 -0.004 F 值 0.14 0.819 △R 2 0.001 0.015 △F 值 0.14 1.498 因变量(Y):Y * p <0.05 ** p <0.01 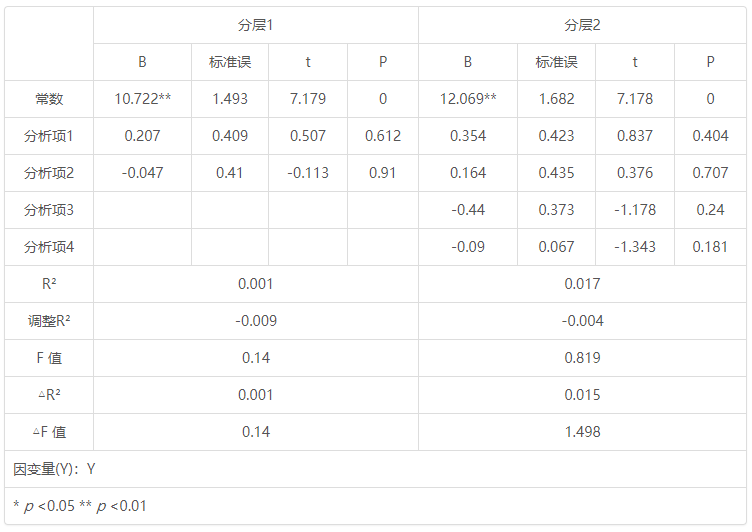
-
-
特别提示
-
分层回归也是回归分析,区别在于分层回归可以得出:分层a到分层b(b=a+1)时R 2变化和F 值变化,便于观察加入新的X时R 2值的变化信息等。
上表格中相当于共有2个回归分析,分析结果表格示例如下:
模型1(分层1) 模型2(分层2) 因变量Y Y Y 自变量 分析项1 分析项1 自变量 分析项2 分析项2 自变量 分析项3 自变量 分析项4 2个回归分析的模型公式分别如下:
Y=10.722+0.207*分析项1-0.047*分析项2
Y=12.069+0.354*分析项1+0.164*分析项2-0.44*分析项3-0.09*分析项4
-
-
SPSSAU操作截图如下:
-
疑难解惑
-
控制变量问题?
-
控制变量指可能干扰模型的项,比如年龄,学历等基础信息。从软件角度来看,并没有“控制变量”这样的名词。“控制变量”就是自变量,如果使用分层回归进行分析,一般情况下“第一层”全部放入控制变量。“第二层”放入核心自变量。
-
另外,控制变量一般是定类数据,理论上控制变量需要作“虚拟(哑)变量”设置,但实际研究中很少这样做而是直接放入模型中,可能原因是“控制变量”并非核心研究项,所以不用考虑太过复杂。
-
中介或者调节作用?
-
如果使用分层回归分析进行中介作用或者调节作用研究,请参考下述两个网页:
-
中介作用: https://www.spssau.com/helps/otherdocuments/mediator.html
-
调节作用: https://www.spssau.com/helps/otherdocuments/moderator.html
-
各项指标的解释?
| 指标 | 意义 |
|---|---|
| R 2 | 模型的解释力度 |
| 调整R 2 | 模型的解释力度(用于惩罚随意放置自变量的指标,一般依旧使用R 2) |
| F 值 | 用于判断模型是否有意义,如果对应p 值小于0.05说明模型有意义 |
| △R 2 | 模型变化时,R 2值的变化情况 |
| △F 值 | 模型变化时,F 值的变化(该值不是直接F 值相减),如果对应p 值小于0.05则说明模型变化有意义,具体可通过△R 2查看模型解释力度变化情况,以及查看新增加的自变量的显著性情况。 |
-
如何进行中介作用或者调节作用研究?
-
同时如果对于调节作用、中介作用的原理理解较少;可直接使用SPSSAU问卷研究-》调节作用、中介作用直接进行智能化分析。
-
F 值括号里面的两个值分别是什么?
-
如果是F 值想计算得到p 值,需要提供两个自由度值df 1和df 2。一般情况下,df 1等于自变量数量;df 2等于样本量 - (自变量数量+1)。此两个值仅为中间过程值,规范格式上需要写成这样而已,无其它实际意义。
-
SPSSAU分层回归时共线性诊断VIF值?
-
SPSSAU进行分层回归时,默认提供VIF值指标,该指标与线性回归一致,通常情况下VIF值小于5(不严格是小于10)即说明没有共线性问题。如果存在共线性问题,可考虑使用‘进阶方法’模块里面的岭回归或者lasso回归进行处理等。
